【图像处理】基于Contour Tracing 方法获取多边形轮廓

https://github.com/xieguigang/sciBASIC

最近在研究实现空间代谢组学中的一些特征区域的自动化划分分割。在得到了特征点集合之后，我们需要根据一些图像处理算法进行特征区域的提取操作。之前，我们尝试过基于绘制等高线图Marching Squares算法的方式来将特征点集合自动转换为特征区域的多边形，实现轮廓扫描获取的功能。但是实现的效果嘛，和实际的区域存在着一些较大的差异。

在Google了一些轮廓算法之后，搜索到了一个在这方面的工作应用上比较合适的方法：Contour Tracing。基于Contour Tracing的方法进行空间代谢组学中的一些特征区域的自动化提取。在Github上，我找到了一个比较好的基于rust语言编写的Contour Tracing方法的实现项目，依照着这个项目，进行了相关的算法的VisualBasic语言上的实现，相关的源代码在这里分享给大家。

A 2D library to trace contours.

https://github.com/STPR/contour_tracing

contours: an array of contours
  ol: outlines level
  hl: holes level
  rn: reachable neighbor - For the outlines: 0: none, 1: front left,  2: front, 3: front right
                         - for the holes:    0: none, 1: front right, 2: front, 3: front left
   o: orientation, e.g. to the east:

          N
    ┏━━━━━━━━━━━┓
    ┃ 7   0   1 ┃
  W ┃ 6   o > 2 ┃ E   o = [2, 3, 4, 5, 6, 7, 0, 1]
    ┃ 5   4   3 ┃
    ┗━━━━━━━━━━━┛
          S

What is Contour Tracing?
Also known as border following or boundary following; contour tracing is a technique that is applied to digital images in order to extract their boundary.

Contour tracing is one of many preprocessing techniques performed on digital images in order to extract information about their general shape. Once the contour of a given pattern is extracted, it's different characteristics will be examined and used as features which will later on be used in pattern classification. Therefore, correct extraction of the contour will produce more accurate features which will increase the chances of correctly classifying a given pattern.

http://www.imageprocessingplace.com/downloads_V3/root_downloads/tutorials/contour_tracing_Abeer_George_Ghuneim/index.html

• Square Tracing Algorithm
• Moore-Neighbor Tracing
• Radial Sweep
• Theo Pavlidis' Algorithm

Moore-Neighbor Tracing算法实现

在轮廓计算算法之中，我们假设一个2D图像上只有两种值：0和1。0表示背景，即无信息的区域，而1表示样本点，即我们所需要进行轮廓计算的目标区域。则根据算法，我们只需要对样本点进行依次扫描即可：

For cursor_y As Integer = 1 To rows
    ol = 1
    hl = 1

    For cursor_x As Integer = 1 To cols
        If ol = hl AndAlso contours(cursor_y)(cursor_x) = 1 Then
            Call trace(True, cursor_x, cursor_y, {2, 3, 4, 5, 6, 7, 0, 1}, 2, (7, 1, 0), O_VERTEX, O_VALUE, contours, paths)
        ElseIf ol > hl AndAlso contours(cursor_y)(cursor_x) = -1 Then
            Call trace(False, cursor_x, cursor_y, {4, 5, 6, 7, 0, 1, 2, 3}, -2, (1, 7, 6), H_VERTEX, H_VALUE, contours, paths)
        End If

        Select Case stdNum.Abs(contours(cursor_y)(cursor_x))
            Case 2, 4, 10, 12
                If contours(cursor_y)(cursor_x) > 0 Then
                    ol += 1
                Else
                    hl += 1
                End If
            Case 5, 7, 13, 15
                If contours(cursor_y)(cursor_x) > 0 Then
                    ol -= 1
                Else
                    hl -= 1
                End If
        End Select
    Next
Next

在进行扫描的时候，由[x, y]所确定下来的一个坐标点P，可以存在有8个访问的方向。所以我们在进行tracing的时候，可以通过传递一个1:8构成的向量来进行访问方向的获取。

Do
    neighbors = {
        contours(tracer_y - 1)(tracer_x),
        contours(tracer_y - 1)(tracer_x + 1),
        contours(tracer_y)(tracer_x + 1),
        contours(tracer_y + 1)(tracer_x + 1),
        contours(tracer_y + 1)(tracer_x),
        contours(tracer_y + 1)(tracer_x - 1),
        contours(tracer_y)(tracer_x - 1),
        contours(tracer_y - 1)(tracer_x - 1)
    }

    rn = getRn(neighbors, outline, o)

    ' ...
Loop

接着呢，我们就可以在坐标点P的基础上，构建出相邻的8个像素点的矩阵用于描绘轮廓信息。在Moore-Neighbor Tracing算法中，我们只需要一直不断地进行递归顺时针访问样本像素点既可以勾勒出对象的轮廓信息。

在改进型的Moore-Neighbor算法之中，对于轮廓上的像素点，我们既可以顺时针的访问像素点的邻居，也可以逆时针的访问像素点的邻居，例如：

contours(tracer_y)(tracer_x) += value(o(0))
tracer_x = tracer_x + MN(o(viv.Item1)).Item1
tracer_y = tracer_y + MN(o(viv.Item1)).Item2
vertices_nbr += 1

' Rotate 90 degrees, counterclockwise For the outlines (rot = 2)
' or clockwise For the holes (rot = -2)
Call o.RotateRight(rot.rem_euclid(8))

If o(0) = 0 OrElse o(0) = 4 Then
    paths.LineTo(tracer_x + vertex(o(0)).Item1, tracer_y)
Else
    paths.LineTo(tracer_x, tracer_y + vertex(o(0)).Item2)
End If

上面所实现的Contour Tracing算法的源代码，大家可以阅读源代码文件MarchingSquares/ContourTracing.vb

在R#脚本中使用Contour Tracing

我已经将所实现的Contour Tracing算法集成在了R#语言的2D图形库之中了，大家可以直接使用contour_tracing函数进行轮廓多边形的获取。使用的方式非常的简单，将目标区域的散点集合的X坐标值和Y坐标值传递进入函数的两个参数即可：

require(graphics2D);

setwd(@dir);

const outline as function(data) {
    const x = data[, "X"];
    const y = data[, "Y"];

    contour_tracing(x, y, 5);
}

const a = read.csv("./region_11.csv", row.names = NULL) |> outline;
const b = read.csv("./region_2.csv", row.names = NULL) |> outline;
const c = read.csv("./region_9.csv", row.names = NULL) |> outline;

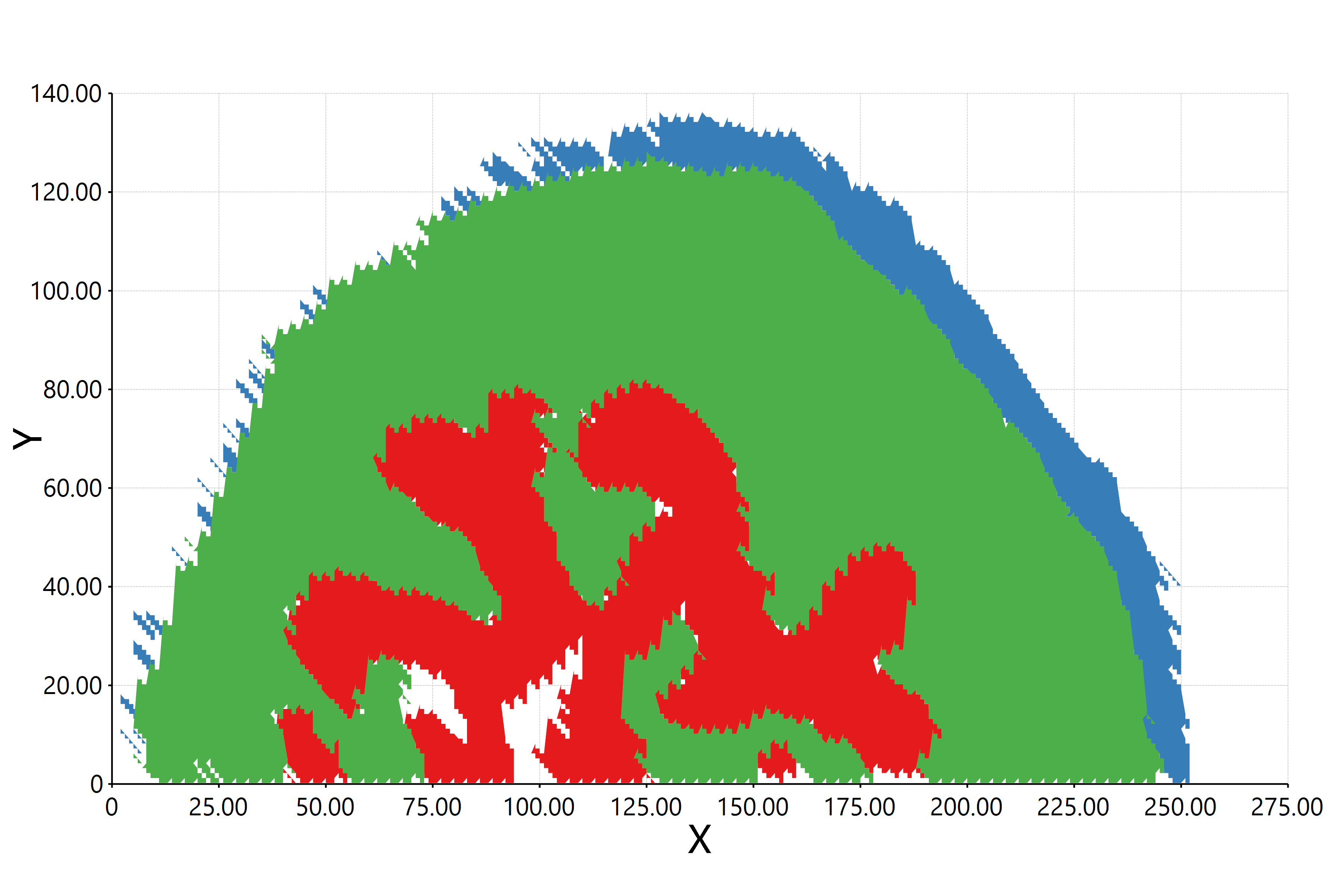
bitmap(file = "./region_unions.png") {
    charts::fillPolygon(list(A = a, B = b, C = c), reverse = TRUE);
}

• Author
• Recent Posts

谢桂纲

高级数据科学家 at 苏州帕诺米克

Working on Engineered bacteria CAD design on its genome from scratch. Writing scientific computing software for Tianhe & Sunway TaihuLight supercomputer. Do scientific computing programming in R/R# language, he is also the programming language designer of the R# language on the .NET runtime.

Latest posts by 谢桂纲 (see all)

• 【MZKit】简单自动化组织分区 - 2023年11月5日
• 【MZKit教程】质谱成像原始数据文件查看 - 2023年6月29日
• 生物序列图嵌入算法 - 2023年6月29日