二叉树聚类

https://github.com/xieguigang/bclusterTree

对于二叉树，大家肯定不会陌生。二叉树其实就是一个有向无环图（有向：访问的方向是从父节点指向子节点；无环：子节点不会成为其父辈节点的父节点），大家可以从根节点一直往下访问到任意一个叶节点；节点间的方向是根据键值的比较的大小结果来建立的，大的值在右边，小的值在左边（《左迁与右迁》），零值在当前节点。

二叉树示意图来自于这篇博文《Self-balanced Binary Search Trees with AVL in JavaScript》

二叉树聚类的原理

假若我们在生成二叉树的时候，在零值的生成过程上我们做一些手脚：我们对二叉树节点键值的计算不再是直接比较大小，而是对键值进行相似度计算，根据阈值来生成大小关系呢？那对于任意两个可以计算出相似度的键值，我们现在就来定下一个规则：

1. 假若这两个键值的相似度比较低，例如，相似度小于0.6，那我们就给比较结果返回一个-1
2. 假若两个键值的相似度非常高，高过了我们所设定的一个阈值，例如相似度大于0.95，以至于我们可以近似的认为二者相等，那这个时候我们就给比较结果返回零
3. 假若相似度计算结果处于上面的两个情形之间，我们就返回1

那，现在应用上面的三个规则到我们的二叉树的建立上，我们会发现，相似度很高的键值都聚集再同一个节点上了；某些键值虽然相似度不高，被分配到了左边或者右边，但是其他的键值可能会和这些键值计算相似度得到一个很高的相似度计算结果，那这些左右节点的键值也都各自递归的聚类再一块了。这就是二叉树聚类的工作原理了。

二叉树聚类的优势

二叉树聚类相对于传统的聚类，其优势就是在于计算规模上很小。例如kmeans，我们会需要做entity之间的pairwise计算，有些时候计算量是会非常的大；假若是单线程的话，一个大数据集的kmeans聚类可能会跑上一整天，甚至更长的时间。

但是对于使用二叉树进行聚类而言，由于二叉树的建立过程本身的特点，我们并不再需要所有的entity都相互比较一次，一般只需要比较计算几次相似度就可以被归为某一个cluster之中了。所以二叉树聚类在大规模的数据集上聚类的效率提升是非常明显的。

但是，我们也不可以说我们可以直接用二叉树聚类来替换掉kmeans聚类，因为虽然二者的计算原理相似（都是计算cluster成员的相似度），但是得到的结果因为计算过程的差异肯定会出现两种算法不一致的结局。这个具体使用哪种算法大家也要具体问题具体分析的看待。

二叉树聚类的应用

在我的工作中，在进行质谱数据处理的时候，做一些代谢物DIA注释的情况下会需要对质谱数据做聚类，建立分子网络，那这个时候我们就可以结合二叉树聚类算法和cos相似度的计算来进行分子网络的快速聚类了。

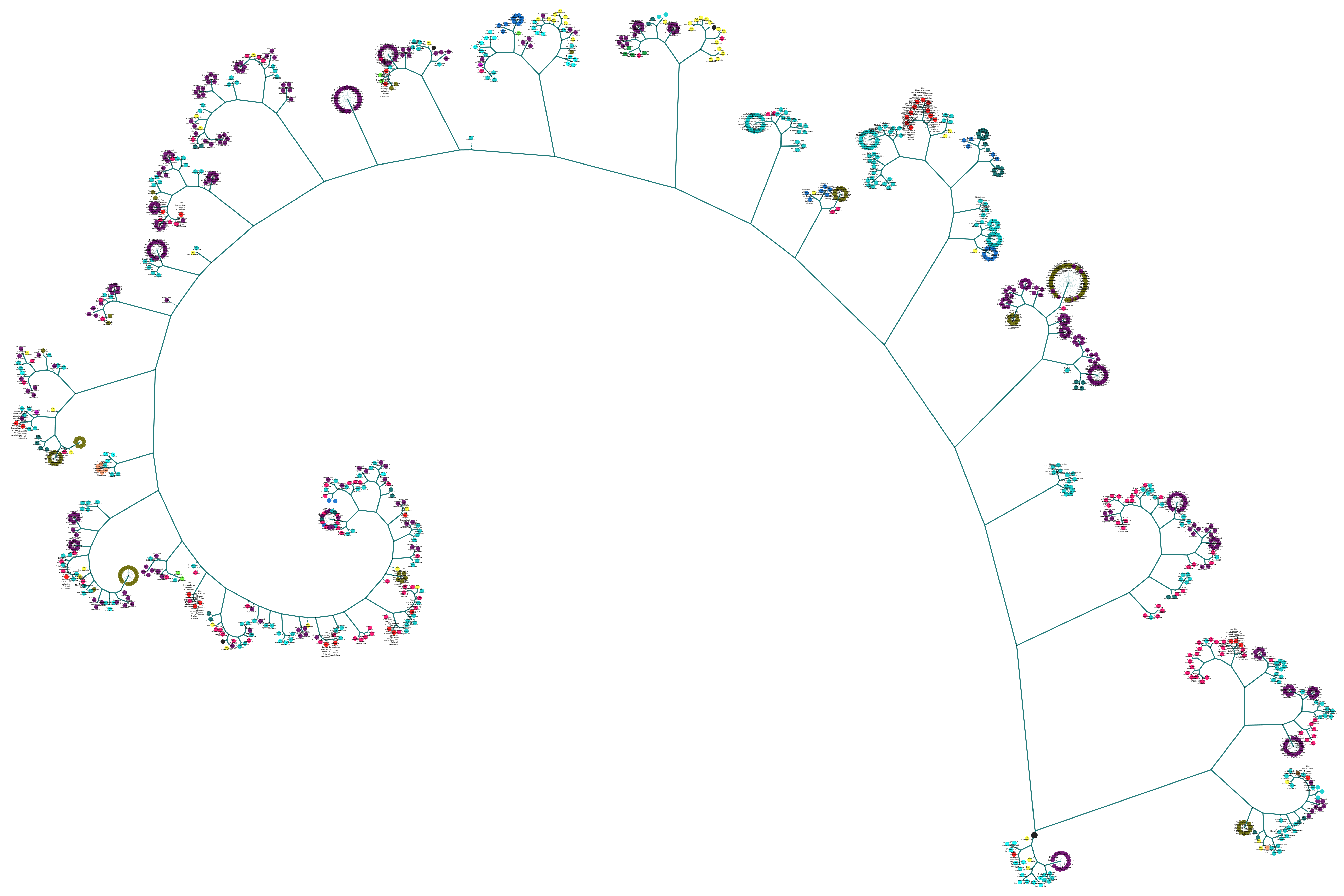
https://github.com/SMRUCC/GCModeller/blob/master/images/phenotypic-bTree-lightbox.png

上面的图就是在比较久之前的做全基因组表达调控网络分析所做的一个通过二叉树聚类建立起的motif-pathway关联的聚类图。可以从全图中看到，调控某一个代谢途径的motif一般都可以在其所调控的基因的表达量上产生很高的关联度，调控同一个pathway的motif往往都可以相互聚类在一块，说明这个二叉树聚类算法的效果还是非常的好的。

使用R语言实现二叉树聚类

我将比较久之前所实现的一个二叉树聚类的代码整理了一下，做出了一个R程序包开源在Github上的bclusterTree项目之中，供大家下载使用。这个程序包的使用方法非常的简单，就是：

1. 我们首先定义一个聚类的索引函数，
2. 然后将索引函数和等待聚类的entity序列一块传递到bcluster函数之中
3. 然后就可以得到聚类结果了，聚类结果是以索引号列表的形式返回的

废话不多说，我们直接上代码例子：假若我们有一个二维坐标的集合，例如

# raw data
x   = runif(100);
y   = runif(100);
seq = lapply(1:length(x), function(i) list(v = c(x[i], y[i])));

然后我们就可以根据欧几里得距离计算出任意两个坐标点之间的距离。假设我们以0.3作为距离的阈值，即小于0.3的距离，就认为两个坐标点是在同一个地方的。所以我们就可以根据这个规则写出下面的索引函数，然后我们就可以将二维坐标点和上面的索引函数传递进入二叉树聚类函数之中了：

# define compares order
index = function(p1, p2) {
    d = sqrt(sum((p1$v - p2$v) ^ 2));

    if (d <= 0.3) {
        0
    } else if (d <= 0.6) {
        1
    } else {
        -1
    }
}

# run clustering
c = bcluster(seq, index);

好了，二叉树聚类一瞬间就跑完了，我们来作图做一下数据可视化，看看聚类的结果怎么样？

# plot result data
plot(x, y, pch = 2, col = "white");

i       = 1;
colors1 = c(
    "red", "blue", "green", "yellow", "steelblue",
    "purple", "black", "orange", "gray", "cyan",
    "pink", "skyblue", "limegreen"
);

for(name in names(c)) {
    points(x[c[[name]]], y[c[[name]]], pch=25, col=colors1[i], bg=colors1[i]);
    i = i + 1;
}

这个结果聚类图挺符合我们的预期目标的。

• Author
• Recent Posts

谢桂纲

高级数据科学家 at 苏州帕诺米克

Working on Engineered bacteria CAD design on its genome from scratch. Writing scientific computing software for Tianhe & Sunway TaihuLight supercomputer. Do scientific computing programming in R/R# language, he is also the programming language designer of the R# language on the .NET runtime.

Latest posts by 谢桂纲 (see all)

• 【MZKit】简单自动化组织分区 - 2023年11月5日
• 【MZKit教程】质谱成像原始数据文件查看 - 2023年6月29日
• 生物序列图嵌入算法 - 2023年6月29日