【基因组学】Motif发现与序列扫描方法

Motif是一段典型的序列或者一个结构。一般情况下是指构成任何一种特征序列的基本结构。通俗来讲，即是有特征的短序列，一般认为它是拥有生物学功能的保守序列，可能包含特异性的结合位点，或者是涉及某一个特定生物学过程的有共性的序列区段。比如蛋白质的序列特异性结合位点，如核酸酶和转录因子。

在一般的情况下，如果我们面对一个全新的基因组，想要做类似于表达调控网络的构建。那么这种情况下，我们一般会从Motif计算开始着手。在进行Motif分析的时候，我们一般会首先通过相应的算法，从整个基因组核酸序列之中提取出保守的Motif片段信息；有了Motif列表之后，我们就可以将Motif与数据库之中已存在的Motif信息作比较，进行Motif注释。这样子呢具有Motif注释结果的位点我们一般就可以找到一些调控的关联信息了。对于其他的没有注释信息的Motif，我们就可能会需要通过实验的手段来发现新的调控关联关系。

Motif位点的无监督聚类

现在我们先来学习怎样从基因组序列之中拿到保守的Motif位点吧。在发现未知的新知识的问题研究方法上，因为没有任何先验知识，所以我们在这里一般是基于无监督聚类的方式进行新的未知Motif的发现。为了进行Motif计算，我们首先需要得到种子。

局部最优比对种子

我们在进行Motif搜索的时候，一般会采用两两局部最优比对的方法产生种子数据。提到两两局部最有比对，那大家肯定会首先想到blastn，而从blastn，大家肯定又可以联想到smith-waterman算法。没错，在这里我们会首先需要通过smith-waterman算法生成局部最优的种子。

Dim seeds As List(Of HSP) = regions _
   .AsParallel _
   .Select(Function(q) regions.seeding(q, param)) _
   .IteratesALL _
   .AsList

在上面的代码之中，regions变量就是我们所输入的基因组中的Fasta序列片段的集合。我们在上面的代码中，对所有的序列片段通过seeding函数进行了两两局部最优比对。其中seeding函数就是针对下面所示的smith-waterman方法的循环调用：

Public Function pairwiseSeeding(q As FastaSeq, s As FastaSeq, param As PopulatorParameter) As IEnumerable(Of HSP)
    Dim smithWaterman As New SmithWaterman(q.SequenceData, s.SequenceData, New DNAMatrix)
    Call smithWaterman.BuildMatrix()
    Dim result = smithWaterman.GetOutput(param.seedingCutoff, param.minW)
    Return result.HSP.Where(Function(seed) seed.LengthHit <= param.maxW)
End Function

在pairwiseSeeding函数中，我们对任意两条序列进行局部最优比较，可以得到一系列的高分区片段。对得到的高分区候选，按照一定的长度做一下过滤之后，就可以用于下游的聚类分析了。

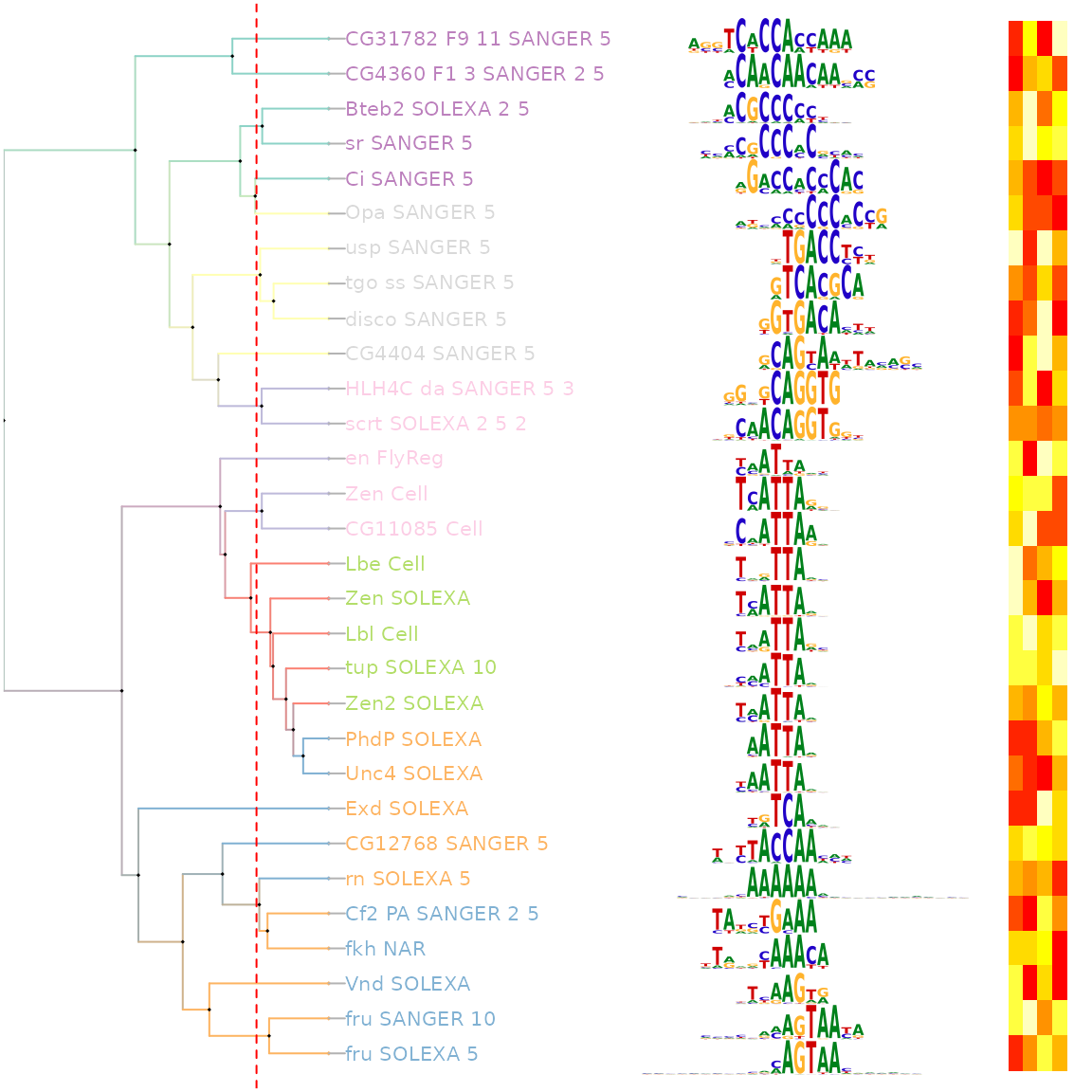
Ou, J., Wolfe, S., Brodsky, M. et al. motifStack for the analysis of transcription factor binding site evolution. Nat Methods 15, 8–9 (2018). https://doi.org/10.1038/nmeth.4555

二叉树聚类

那我们现在通过上面的smith-waterman算法得到的一系列的高分区种子之后，下面我们就可以基于这些高分区种子做无监督聚类。在这里，我们可以基于二叉树进行无监督聚类操作：

Dim tree = seeds _
   .Select(Function(q) New NamedValue(Of String)(q.Query, q.Query)) _
   .BuildAVLTreeCluster(param.seedingCutoff)

在上面的代码之中，我们对高分区片段按照一定的算法计算出相似度，基于相似度进行二叉树构建的过程，就是一个无监督的聚类过程了。为什么不用常见的kmeans做无监督聚类？这个是因为kmeans聚类方法是一种半监督方法，kmeans中我们一般会需要手动指定参数k，过大或者过小的参数k都会导致聚类的结果不符合我们的需求，所以k值的设定我们一般会根据经验来做设定。其次，kmeans是基于一个距离矩阵来完成聚类的，所以在进行kmeans之前，我们还需要将我们的种子之间在进行两两距离计算，生成一个大矩阵才可以进行kmeans。对于一个普通的细菌基因组而言，我们可以得到的种子数量一般会在好几十万个，这就会导致我们整个的计算开销非常的大了。

根据二叉树聚类的思想，我们就可以根据相似度计算结果设定阈值，产生对应的分支:

<Extension>
Public Function BuildAVLTreeCluster(seeds As IEnumerable(Of NamedValue(Of String)), Optional cutoff# = 0.95) As BinaryTree(Of String, String)
    Dim divid# = cutoff / 2
    Dim cluster As New AVLTree(Of String, String)(
        Function(q, s)
            Dim SSM# = SeedCluster.Compare(q, s)

            If SSM >= cutoff Then
                Return 0
            ElseIf SSM >= divid Then
                Return 1
            Else
                Return -1
            End If
        End Function, Function(s) s)

    For Each seed As NamedValue(Of String) In seeds
        Call cluster.Add(seed.Value, seed.Name, valueReplace:=False)
    Next

    Return cluster.root
End Function

从上面的代码中我们可以看得到，对于任意两个高分区种子之间，我们可以采用余弦相似度做计算函数，得到SSM余弦相似度。之后呢，就可以将大于0.95预设值的比对结果当作为相等的情况，大于0.95/2的结果作为右分叉的情况。这样子就可以产生聚类结果了。由于二叉树聚类与Kmeans相比较，我们并不需要根据经验设定k值，不会人为干预最终的聚类结果数量；而是按照需求设定具体的树枝的分支阈值，二叉树聚类得到的聚类结果数量完全就是根据数据本身的组成而自动产生的，这就是一个完全的无监督自动化聚类的过程了。

在进行上面的余弦相似度得分计算的过程之中，由于我们需要比较两个高分区片段之间的相似度，所以在这里我们会需要通过NeedlemanWunsch全局最优比对来完成计算：

<Extension>
Public Function ScoreVector(compares As (q$, s$)) As (q As Vector, s As Vector)
    Dim query As New FastaSeq With {.SequenceData = compares.q.ToUpper, .Headers = {"query"}}
    Dim subject As New FastaSeq With {.SequenceData = compares.s.ToUpper, .Headers = {"subject"}}
    Dim globalAlign As GlobalAlign(Of Char) = RunNeedlemanWunsch.RunAlign(query, subject, 0).First
    Dim q = globalAlign.query.AsEnumerable
    Dim s = globalAlign.subject.AsEnumerable
    Dim a As New List(Of Double)
    Dim b As New List(Of Double)

    For Each nt As SeqValue(Of (q As Char, s As Char)) In (q, s).SeqTuple
        With nt.value.ScoreTuple
            Call a.Add(.a)
            Call b.Add(.b)
        End With
    Next

    Return (a.AsVector, b.AsVector)
End Function

根据上面的NeedlemanWunsch全局最有比对方法，我们可以得到两个等长的得分向量。这样子我们就可以基于这两个等长向量做余弦相似度计算。

产生PWM矩阵

通过二叉树聚类操作之后，每一个二叉树结点都是一个相似度非常高的种子的集合。那我们的Motif的PWM（Position Weighted Matrix）矩阵就是基于这些高度保守的种子所产生的。由于这些种子保留片段之间的长度可能会不一样，所以在这里我们会首先需要对这些同一个二叉树节点中的种子片段做一次多序列比对。通过多序列比对之后，我们就可以将序列片段都变成等长片段了。基于这些等长片段，我们就可以非常容易的建立碱基的位置概率分布矩阵，即PWM矩阵。

<Extension>
Private Function motif(group As BinaryTree(Of String, String),
                       regions As FastaSeq(),
                       param As PopulatorParameter) As SequenceMotif

    Dim members As List(Of String) = group!values
    Dim MSA As MSAOutput = members _
        .Select(Function(seq)
                    Return New FastaSeq With {
                        .SequenceData = seq,
                        .Headers = {""}
                    }
                End Function) _
        .MultipleAlignment(Nothing)
    Dim PWM As SequenceMotif = MSA.PWM(members:=regions, param:=param)

    Return PWM
End Function

在通过多序列比对之后，基于多序列比对的结果建立PWM矩阵的过程，顾名思义，我们只需要按照位置统计出各种残基的出现频率即可：

Dim residues As New List(Of Residue)
Dim nt = {"A"c, "T"c, "G"c, "C"c}
Dim MSA As String() = alignment.MSA

For i As Integer = 0 To MSA(Scan0).Length - 1
    Dim index% = i
    Dim P = MSA _
        .Select(Function(seq) seq(index)) _
        .GroupBy(Function(c) c) _
        .ToDictionary(Function(c) c.Key,
                      Function(g)
                          Return g.Count / MSA.Length
                      End Function)
    Dim Pi = nt.ToDictionary(
        Function(base) base,
        Function(base)
            Return P.TryGetValue(base)
        End Function)

    residues += New Residue With {
        .frequency = Pi,
        .index = i
    }
Next

Motif序列位点扫描方法

现在我们已经通过一系列的序列通过相似度聚类分析以及序列全局比对对齐之后，得到了一系列的Motif聚类结果数据。实际上这些Motif数据都是对位点上的碱基所出现的概率值的统计结果。那现在假若我们需要将目标核酸序列上可能属于这些Motif位点的位置给扫描出来，有什么比较方便的方法呢。

实际上，对于这个所需要的位点扫描功能，我们可以直接通过smith-waterman局部最优序列比对方法来完成。如果我们将实际的核酸序列外推至更加一般的数据模型，实际上我们就可以发现，一条核酸碱基组成上已经非常确定的序列数据，其实就是对应的位点上某一种碱基的出现概率值总为100%的一个PWM矩阵。

在进行序列两两比较的时候，我们的动态规划算法在进行得分计算的时候，当两个所比较的碱基一致的时候，将会得到一个高分，反之当两个所比较的碱基不一样的时候，我们会根据对应的罚分矩阵设置一个罚分值。这样子我们就可以通过对应的动态规划方法得到具体的序列比对结果。

那现在我们在更加一般的序列数据结构基础上来看待这个序列两两比较问题的解决方法，假设我们现在并不是直接比较两个碱基的字符等价性来得到具体的分数，而是通过一个具体的概率值的打分计算。

Smith-Waterman局部最优比对方法

为了方便理解基于Smith-Waterman方法进行Motif位点扫描，现在我们基于sciBASIC框架之中的Smith-Waterman动态规划框架来讲解序列比对。现在我们有这样子的一个残基模型：

Private Shared Function SymbolProvider(blosum As Blosum) As GenericSymbol(Of Char)
    Return New GenericSymbol(Of Char)(
        equals:=Function(x, y) x = y,
        similarity:=AddressOf (blosum Or blosum62).GetDistance,
        toChar:=Function(x) x,
        empty:=Function() "-"c
    )
End Function

可以看得见，在一般的正常序列比对操作过程之中，我们是直接通过Fasta序列之中的残基字符的等价性来直接做判断的。这样子的话，x与y两个字符相等则直接判定为对应的残基相同；假若不一样的话，则会通过blosum矩阵得到一个得分。

那现在按照上面所介绍的思路，我们现在将残基字符转换为对应的概率值，用于进行Motif位点扫描的话，可以有：

Dim symbol As New GenericSymbol(Of Residue)(
    equals:=Function(a, b) Compare(a, b) >= 0.85,
    similarity:=AddressOf Compare,
    toChar:=AddressOf Residue.Max,
    empty:=AddressOf Residue.GetEmpty
)

在上面的代码之中，Residue类型为PWM矩阵之中的一列数据，其数据结构大致如下所示：

Public Structure Residue
    Public Property frequency As Dictionary(Of Char, Double)
    Public Property index As Integer
End Structure

主要包括碱基符号出现的概率，以及当前的残基在Motif上的位置编号。在上面的符号创建的过程之中，引用了一个Compare函数，这个Compare函数则是会用于计算两个Residue残基对象之间的相似度，最常见的计算方式就是计算frequency向量的cos相似度了。

从上面的对残基符号的定义代码来看，假若两个残基对象a和b之间的cos相似度大于0.85，则认为二者等价。反之，则会使用对应的cos相似度值作为对应序列位置处的Smith-Waterman动态规划算法的得分结果值。阅读完上面的代码，现在是不是已经能够理解了我们是如何做Motif扫描的么？

使用GCModeller进行Motif发现

在GCModeller程序包之中，已经通过R#程序包的方式提供了上面的Motif计算方法，相应的编程接口如下所示：

''' <summary>
''' find possible motifs of the given sequence collection
''' </summary>
''' <param name="fasta"></param>
''' <param name="minw%"></param>
''' <param name="maxw%"></param>
''' <param name="nmotifs%"></param>
''' <param name="noccurs%"></param>
''' <returns></returns>
<ExportAPI("find_motifs")>
Public Function GetMotifs(<RRawVectorArgument> fasta As Object,
                          Optional minw% = 6,
                          Optional maxw% = 20,
                          Optional nmotifs% = 25,
                          Optional noccurs% = 6,
                          Optional env As Environment = Nothing) As SequenceMotif()

    Dim param As New PopulatorParameter With {
        .maxW = maxw,
        .minW = minw,
        .seedingCutoff = 0.95,
        .ScanMinW = 6,
        .ScanCutoff = 0.8
    }
    Dim motifs As SequenceMotif() = GetFastaSeq(fasta, env) _
        .PopulateMotifs(
            leastN:=noccurs,
            param:=param
        ) _
        .OrderByDescending(Function(m) m.score / m.seeds.MSA.Length) _
        .Take(nmotifs) _
        .ToArray

    Return motifs
End Function

从上面的代码之中可以看得到，在相应的Motif查找方法的参数之中，最主要的一个参数就是接受Fasta序列数据。如果想要使用上面的函数进行序列Motif计算，我们会需要首先获取得到一个Fasta序列集合对象，然后传递进入这个函数即可，使用起来非常的方便：

# ["LexA.fasta"]
seq
|> read.fasta
|> find_motifs(minw = 6, maxw = 10)
|> lapply(function(motif) {
    motif
    |> json(compress = FALSE)
    |> writeLines(con = `${export}/${motifString(motif)}.json`)
    ;

    bitmap(file = `${export}/${motifString(motif)}.png`) {
        plot(motif);
    };
})
;

在上面的流程代码之中，seq变量是Fasta序列文件的文件路径。我们在使用read.fasta函数读取完对应的核酸序列之后，就可以得到一个Fasta序列对象集合，然后将这个Fasta序列集合传递进入Motif查找函数之中即可。最后将我们得到的每一个Motif数据都序列化为json文件以及通过plot函数绘制出来。在命令行中执行上面的脚本，我们可以得到大概如下所示的候选输出。和最开始的序列输出比较一下，通过这个方法得到的Motif输出的相似度是非常高的：

• Author
• Recent Posts

谢桂纲

高级数据科学家 at 苏州帕诺米克

Working on Engineered bacteria CAD design on its genome from scratch. Writing scientific computing software for Tianhe & Sunway TaihuLight supercomputer. Do scientific computing programming in R/R# language, he is also the programming language designer of the R# language on the .NET runtime.

Latest posts by 谢桂纲 (see all)

• 【MZKit】简单自动化组织分区 - 2023年11月5日
• 【MZKit教程】质谱成像原始数据文件查看 - 2023年6月29日
• 生物序列图嵌入算法 - 2023年6月29日