文章阅读目录大纲
![]() https://github.com/xieguigang/sciBASIC
https://github.com/xieguigang/sciBASIC
在进行无监督聚类分析的方法之中,我们在算法代码之中一般会遇到求解与某一个样本数据点最相似的数据点的计算过程。对于这个计算过程,一般而言我们是基于欧几里得距离来完成的。
但是,使用欧几里得距离对于高维度的样本数据的计算而言,由于维度灾难的存在,对于基于欧氏距离的聚类算法在计算时间上的成本会特别高。
![]()
![]()

对于任意两个等长的样本数据点向量,存在有二阶的闵可夫斯基距离(Minkowski distance),即欧几里得距离。
基于欧几里得距离进行数据样本点分类的最简单的一个算法就是K-近邻(KNN)算法。K-近邻算法是一种典型的无参监督学习算法,对于一个监督学习任务来说,其m个训练样本为:
![]()
基于上面的m个数据样本点,我们无需利用训练样本学习出统一的模型。例如,对于一个新的样本,如X,我们一般是可以直接通过比较样本X与m个训练样本的相似度,选择出k个欧几里得距离最小的样本,并以这k个样本的标签作为样本X的标签。好吧,我忘了说了,在上面的一个基于欧几里得距离比较样本的相似度来打标签的过程其实会需要我们暴力的将样本点X与m个训练样本都比较计算一次。假若有n个样本X,则会需要计算n*m
KD树与K邻近点计算
在讲解KD树之前,我们先回到一个较为简单的数据查找问题来进行KD树算法的讲解。我们进行数据查找的时候,最简单的一个方法是不是首先想到的就是基于一个For循环挨个比对我们的数据对象来实现的呢?那,这个通过For循环暴力查找的方法虽然简单,但是效率不高,因为最坏的情况要比对N次。为了解决查找的效率问题,前人提出了基于二叉树的查找方法。通过二叉树对数据序列的递归二分查找,这样子我们就可以一下子将N次计算缩短为O(n)

实际上我们基于二叉树,也可以直接进行聚类分析。关于使用二叉树的聚类操作,大家可以阅读我之前的博文:《二叉树聚类》
上面说的二叉树,一般而言是只处理一个维度的key的比较。对于KD树而言,我们通过其英文全称(k-dimensional tree)也可以很直观的了解到KD树是针对K个维度的二叉树,基于对k维空间的一个划分,实现基于K个维度的key的数据查找操作。为什么是这样子说的呢?我们可以看下面的一些原理图:

我们在这里以一个二维的数据来说明KD树的建立过程。假设我们有上面的一系列数据点需要放入KD树之中。
- 则我们最开始可以先对X维度做二分分割:在上图中的root节点中,X等于7,所以我们可以将所有X小于7的数据点都放到左边,X大于7的数据点都放到右边。这样子就构建出了一个以X维度为key的二叉树。
- 接着呢,我们继续分别对左边以及右边所划分出来的数据点做Y维度的二分分割:以左边的数据点为例,第二排的数据点中,Y维度的值为4,所以我们可以将左边的数据中,Y小于4的都继续放到左边,Y大于4的数据点都放到右边
- 这样子呢,我们只需要递归的重复执行上面的两个步骤,就可以对数据点中的每一个维度都建立了二叉树。这个时候,我们所建立的二叉树就是KD树。

我们将上面的二维数据点的二叉树建立的过程中,维度的转换过程在一个平面上可视化出来,就可以得到上面的一个对整个平面进行二分划分的可视化结果图。例如红色的竖线就表示在建立二叉树过程中,对X维度的二分分割。蓝色的水平线就是表示对Y维度的二分分割。
上面所描述的建立KD树的过程,可以使用下面的VB代码来表示出来:
Private Function buildTree(points As T(), depth As Integer, parent As KdTreeNode(Of T)) As KdTreeNode(Of T)
Dim axis = depth Mod dimensions.Length
Dim median As Integer
Dim node As KdTreeNode(Of T)
If points.Length = 0 Then
Return Nothing
ElseIf points.Length = 1 Then
Return New KdTreeNode(Of T)(points(Scan0), axis, parent)
Else
' sort by the axis dimensions
points.Sort(Function(a, b)
Return access(a, dimensions(axis)) - access(b, dimensions(axis))
End Function)
_counts += 1
median = stdNum.Floor(points.Length / 2)
End If
Dim left = points.slice(0, median).ToArray
Dim right = points.slice(median + 1).ToArray
node = New KdTreeNode(Of T)(points(median), axis, parent)
node.left = buildTree(left, depth + 1, node)
node.right = buildTree(right, depth + 1, node)
Return node
End Function在上面的代码中,depth Mod dimensions.Length
Dim left = points.slice(0, median).ToArray
Dim right = points.slice(median + 1).ToArray即,我们对数据序列按照所设定的某一个维度升序排序后,从中间分隔开即可实现二叉树分割。
KD树查找
既然我们实现KD树的目的就是需要实现K个维度上的快速查找操作。那在这里就必须要说一下基于KD树的查找过程了。
首先,在维度自动转换上,我们会需要按照建树的时候一样的规则写下如下的转换规则代码:
Dim dimension As Integer = depth Mod dimensions.Length
Dim axis As String = dimensions(dimension)然后呢,我们就可以基于此维度进行二叉树查找操作,例如:
' whats got the got best _search result? left or right?
Dim goLeft = access(node.data, axis) < access(point.data, axis)
Dim target = If(goLeft, node.left, node.right)
Dim opposite = If(goLeft, node.right, node.left)上面代码说的就是,当目标数据点在当前维度的数据要小的话,我们就在左边的树中做查找,反之在右边做查找。是不是已经发现了,上面的过程就是和二叉树查找的过程一摸一样的!
' target has our most likely nearest point, we go down that side of the
' tree first
If Not target Is Nothing Then
Call nearestSearch(point, target, depth + 1, result, maxNodes)
End If
' _search the opposite direction, only if there is potentially a better
' value than the longest distance we already have in our _search results
If Not opposite Is Nothing AndAlso opposite.distanceSquared(point.data, access) <= result(result.Count - 1).distance Then
Call nearestSearch(point, opposite, depth + 1, result, maxNodes)
End If对于二叉树的查找过程,我们只需要递归的执行下去整个查找过程就可以了。这里实现的完整的代码,大家可以阅读源代码文件:【KdTree.vb】中的nearestSearch
那,现在有了KD树之后,我们就可以很高效率的进行KNN的聚类计算分析了。也就是说,我们通过KD树,可以以很高的效率对高维度的数据进行数据查找。例如在使用PhenoGraph方法进行单细胞测序的数据处理过程之中,就首先使用上了KD树进行KNN数据点的查找,产生K个维度的Feature向量,用于通过杰卡德相似度构建出一个相关性矩阵。
KD树可视化
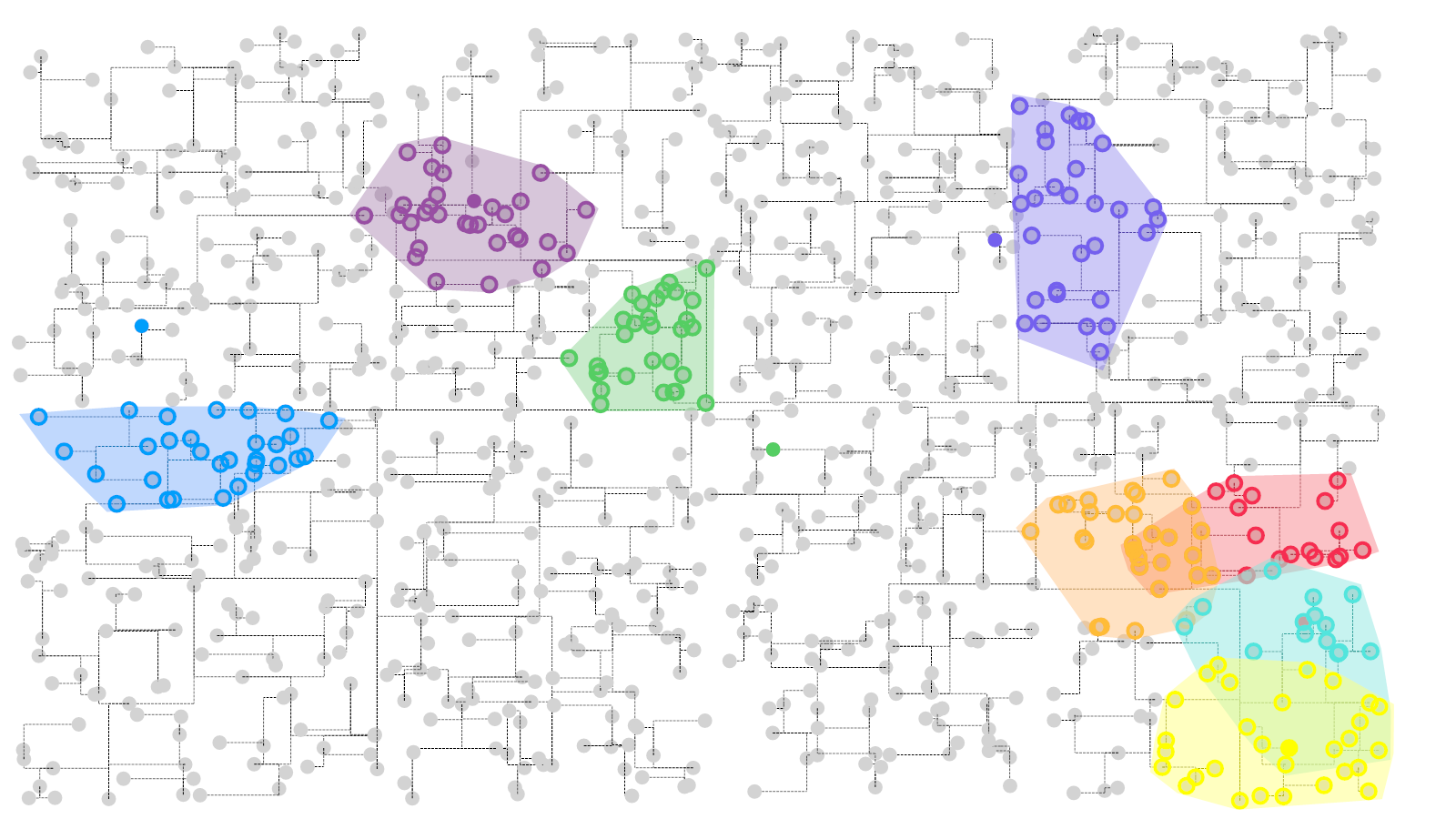
基于上面所实现的KD树代码,我们可以对一个随机的二维空间的数据点建立KD树,然后抽取随机数据点进行K个临近点的查找,将KNN结果点标记出来来可视化我们的算法的执行效果:
Dim size As New Size(3600, 2700)
Dim points2 As Point2D() = 1000 _
.SeqRandom _
.Select(Function(i)
New Point2D(randf.NextInteger(size.Width), randf.NextInteger(size.Height))
End Function) _
.ToArray
Dim tree As New KdTree(Of Point2D)(points2, New PointAccess)
Dim query = {
New NamedValue(Of PointF)("1", points2.Random, "#009EFB"),
New NamedValue(Of PointF)("1", points2.Random, "#55CE63"),
New NamedValue(Of PointF)("1", points2.Random, "#F62D51"),
New NamedValue(Of PointF)("1", points2.Random, "#FFBC37"),
New NamedValue(Of PointF)("1", points2.Random, "#7460EE"),
New NamedValue(Of PointF)("1", points2.Random, "#52E5DD"),
New NamedValue(Of PointF)("1", points2.Random, "#984ea3"),
New NamedValue(Of PointF)("1", points2.Random, "#ffff00")
}
Call DrawKDTree _
.Plot(tree, query, k:=30, size:="1600,900", padding:="padding: 20px 20px 20px 20px;") _
.Save("/path/top/demo_visual.png")
- R#环境中的热图颜色 - 2025年6月11日
- HE染色结果怎么看 - 2025年6月10日
- 脂质组学概述 - 2025年6月10日


One response
[…] 对于KD树的讲解,大家可以阅读之前的博客文章《【机器学习】K-D树介绍》 […]