文章阅读目录大纲
 https://github.com/xieguigang/sciBASIC/
https://github.com/xieguigang/sciBASIC/
线性规划(Linear programming,简称LP),是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支,它是辅助人们进行科学管理的一种数学方法。研究线性约束条件下线性目标函数的极值问题的数学理论和方法。
在系统生物学领域内,有着一个非常经典的FBA(Flux Balance Analysis)方法进行代谢网络的数学建模分析。FBA方法是基于线性规划进行代谢网络最优化问题的求解。在这里我来为大家介绍一下在GCModeller软件包之中对FBA问题进行线性规划求解的计算引擎的开发。

Illustration of genome-scale metabolic reconstruction and flux balance analysis.
- a. Genome-scale metabolic reconstructions are built in two steps. First, several platforms exist for the generation of a gap-filled draft metabolic reconstruction based on genome annotations. Second, the draft reconstructions need to be refined based on known experimental and biochemical data from literature 7. Novel experiments can be performed on the organism and the reconstruction refined accordingly.
- b. In flux balance analysis (FBA), the metabolic reconstruction containing n reactions and m metabolites is converted to a stoichiometric matrix S. FBA solves an optimization problem where an objective function Z is maximised or minimised. Z is formed by multiplying every reaction flux vi with a predetermined constant, ci, and adding the resulting values. FBA solves a steady state, Sv = 0. Every reaction i is bound by two values, an upper bound (ubi) and lower bound (lbi).
- c. The solution space is defined by the mass balanced constraints imposed for the upper and lower bounds of each reaction in the metabolic reconstruction. Optimisation for a biological objective function (e.g. biomass production, ATP consumption, heme production, etc.) identifies an optimal flux within the solution space, whereas uniform sampling provides an unbiased characterisation by sampling candidate fluxes distributed in the solution space.
Creation and analysis of biochemical constraint-based models: the COBRA Toolbox v3.0 DOI:10.1038/s41596-018-0098-2

线性规划问题描述
在线性规划数学模型中,一般我们能够找到决策变量很多个解。即有很多种方案,在这里我们以仅包含有两个变量的线性规划模型为例,将所有约束条件用图形绘出:

图中的彩色线段为约束条件,这些线段所围成的一个多边形为可行解。这个图中所示的变量只有[x1, x2]两个变量的线性规划问题。
对于上图所示的一个简单线性规划问题而言,一般会存在有以下几种解:
- 【可行解】凡满足所有约束条件的所有解称为可行解,它们对应可行方案。所有可行解的集合构成可行解域。即图中阴影部分。可行解域中的任何一点称为可行点,对应一个可行方案,这个点的坐标[x1, x2]构成一个列向量,称为可行向量。
- 【最优解】凡使得目标函数Z值达到最优(最大或最小)的可行解称为最优解。最优解一般情况下是唯一存在的,但在一些特殊的规划问题中,可能有无穷多个最优解或者不存在最优解。
- 【基本解】所有约束条件直线的交点对应的解称为基本解。
- 【基本可行解】可行解域边界上的约束条件直线的交点对应的解称为基本可行解,即上图中所有约束条件线段相交的点对应的解。它满足两个条件:其一是基本解,即约束条件直线的交点对应的解;其二是可行解,即满足所有的约束条件,在可行解域内。
从结构上看,线性规划数学模型包括目标函数、约束条件和变量非负约束三个部分。完整的表达式为:

单纯形法求解线性规划问题(Simplex Method)
单纯形法是1947年美国数学家丹捷格(G.B.Dantzig)提出的一种用于一般线性规划问题求解的方法。单纯形法首先要做的就是把方程化为标准形式:
- 所有的变量都是非负数
- 所有的约束都是等式(非负限制除外),且具有非负的右端项

在这里我们以一个简单实例来讲解单纯形法的计算机代码实现。假设我们有一个简单的线性规划问题,如下所示:

首先,我们需要对非等号的约束条件引入松弛变量(Slack)以及对等号的约束条件引入人工变量来将上面的问题转换为标准形式(将不等式constraints转成等式):

相应的代码实现如下所示,在这里我们只需要对不是等号的约束条件引入松弛变量即可:
''' <summary>
''' Change Signs to = by adding variables
''' </summary>
Friend Sub makeStandardForm()
For i As Integer = 0 To constraintTypes.Length - 1
If constraintTypes(i) <> "=" Then
addVariableAt(i, If(constraintTypes(i) = "≥" OrElse constraintTypes(i) = ">=", -1, 1))
constraintTypes(i) = "="
End If
Next
End Sub
''' <summary>
''' Unfortunate copy and pasting going on here.
''' </summary>
''' <param name="constraintIndex"></param>
''' <param name="value"></param>
Private Sub addVariableAt(constraintIndex As Integer, value As Double)
variableNames.Add("v" & subscriptN(variableNames.Count + 1))
objectiveFunctionCoefficients.Add(0)
For j As Integer = 0 To constraintCoefficients.Length - 1
constraintCoefficients(j).Add(If(j <> constraintIndex, 0, value))
Next
End Sub引入的松弛变量的符号是和约束条件有关的。例如,对于一个
>=符号的约束条件而言,转换为等式的时候,我们至少要保证条件的左边减掉任意一个数之后应该满足右边的约束值。所以对于>=符号的约束条件的符号为负值;反之对于<=,我们应该至少要保证条件的左边加上任意一个数之后任然是应该满足右边的约束值,所以其符号为正号。
引入松弛变量之后,再对剩余的等号的表达式引入人工变量:
Friend Function ArtificialVariableAssignments() As List(Of Integer)
Dim assignments As New List(Of Integer)()
Dim k As Integer = 0
For j As Integer = 0 To constraintTypes.Length - 1
If constraintTypes(j) = "=" Then
assignments.Add(objectiveFunctionCoefficients.Count + k)
k += 1
Else
assignments.Add(-1)
End If
Next
Return assignments
End Function
Friend Sub addArtificialVariables(artificialVariables As List(Of Integer))
For j As Integer = 0 To constraintTypes.Length - 1
If artificialVariables(j) <> -1 Then
Me.addVariableAt(j, 1)
End If
Next
End Sub对上面的示例问题做转换对齐以后,可以得到一个矩阵:

x4为松弛变量,x5,x6为人工变量
可以看到,在最开始的时候,x4=2,x5=4,x6=0。变量X2的系数为4,是所有变量中系数值最大的。取X2为基变量:
Private Function findInitialBasicVariables(artificialVariables As List(Of Integer)) As List(Of Integer)
' Declare Basic Variable array, boolean to indicate if a feasible solution has been found
Dim alpha As New List(Of Integer)()
Dim foundBasicFeasSol As Boolean = False
' Determine the number of regular variables
Dim q As Integer = 0
For j As Integer = 0 To artificialVariables.Count - 1
If artificialVariables(j) <> -1 Then
q += 1
End If
Next
' Set up parameters for finding subsets
Dim n As Integer = lpp.variableNames.Count - q
Dim powerSetSize As Integer = CInt(Fix(stdNum.Pow(2, n)))
For i As Integer = 0 To powerSetSize - 1
' Reinitialize potential basic feasible solution
alpha = New List(Of Integer)()
' Convert the binary number to a string containing n digits
Dim binary As List(Of Char) = intToBinary(i, n)
' Create the corresponding subset
For j As Integer = 0 To binary.Count - 1
If binary(j) = "1"c Then
alpha.Add(j)
End If
Next
' Check to see if the basic variable set alpha is feasible
If alpha.Count = lpp.constraintRightHandSides.Length AndAlso isFeasible(alpha) Then
foundBasicFeasSol = True
Exit For
End If
Next
' No feasible solution is found, create dummy solution vector.
If Not foundBasicFeasSol Then
alpha = New List(Of Integer)()
For j As Integer = 0 To lpp.constraintRightHandSides.Length - 1
alpha.Add(-1)
Next
End If
Return alpha
End Function这个时候我们看X2对应的列,就可以得到x2=2*x4+4*x5+0*x6

进行上面所描述的行列式计算,我们可以通过一个While循环来执行:
Do While go
' Get next variable to pivot on
Dim n As Integer = choosePivotVar(artificialVariables)
Dim [next] As Integer = choosePivotConstraint(n)
' If optimal solution reached, end 'while' statement
If n = -1 Then
' Found a solution. Stop pivoting.
go = False
ElseIf limiter = LPP.PIVOT_ITERATION_LIMIT Then
' Check iteration limit not exceeded.
Return New LPPSolution("The pivot max iteration cap was exceeded.", solutionLog.ToString, feasibleSolutionTime)
ElseIf [next] = -1 Then
' Check for unboundedness.
Return New LPPSolution("The given LPP is unbounded.", solutionLog.ToString, feasibleSolutionTime)
Else
' Get pivot constraint, continue.
pivot(n, [next])
basicVariables([next]) = n
solutionLog.AppendLine("Pivot at " & n & ", " & [next])
End If
Loop我们可以看到,这个时候我们之前所引入的人工变量x5和x6的值都变为零了。使用主元消去法:


得到了最优解。上面的代码过程,大家可以阅读源文件【LPPSolver.vb】。
R#脚本实例
在R#
imports "lpSolve" from "Rlapack";
const objective = ~x1 + 9 * x2 + x3;
const subject_to = ~[
x1 + 2 * x2 + 3 * x3 = 9,
3 * x1 + 2 * x2 + 2 * x3 = 15
];
const lpp = lp("max", objective, subject_to);
str(lpp$solution);
print("objective value:");
print(lpp$objective);
# List of 3
# $ x1 : num 3
# $ x2 : num 3
# $ x3 : num 0
#
# [1] "objective value:"
# [1] 30
- R#环境中的热图颜色 - 2025年6月11日
- HE染色结果怎么看 - 2025年6月10日
- 脂质组学概述 - 2025年6月10日

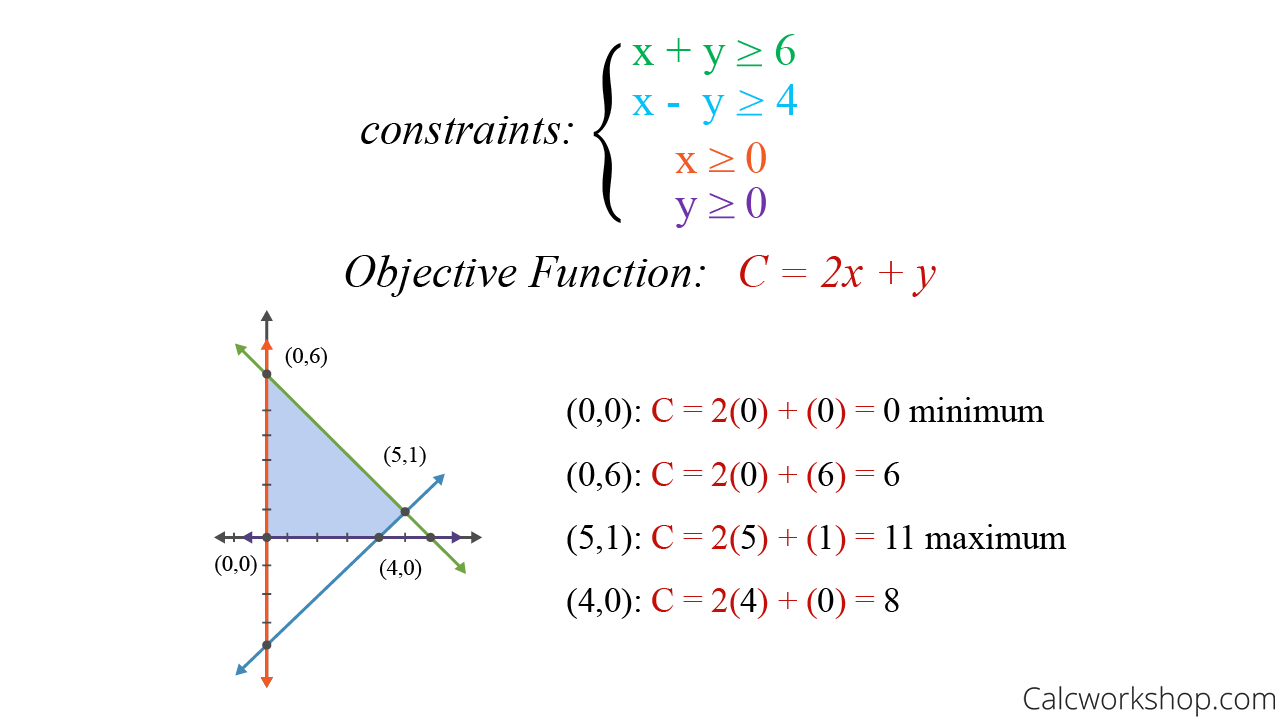

One response
[…] 关于线性规划计算的原理,大家可以阅读博客文章《使用R#语言求解线性规划问题》,里面有比较详细的原理说明以及代码实现介绍。 […]