估计阅读时长: 16 分钟https://github.com/xieguigang/sciBASIC/ 线性规划(Linear programming,简称LP),是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支,它是辅助人们进行科学管理的一种数学方法。研究线性约束条件下线性目标函数的极值问题的数学理论和方法。 Order by Date Name Attachments linear-programming-example • 22 kB • 382 click 2021年8月11日lppsolve_screen […]
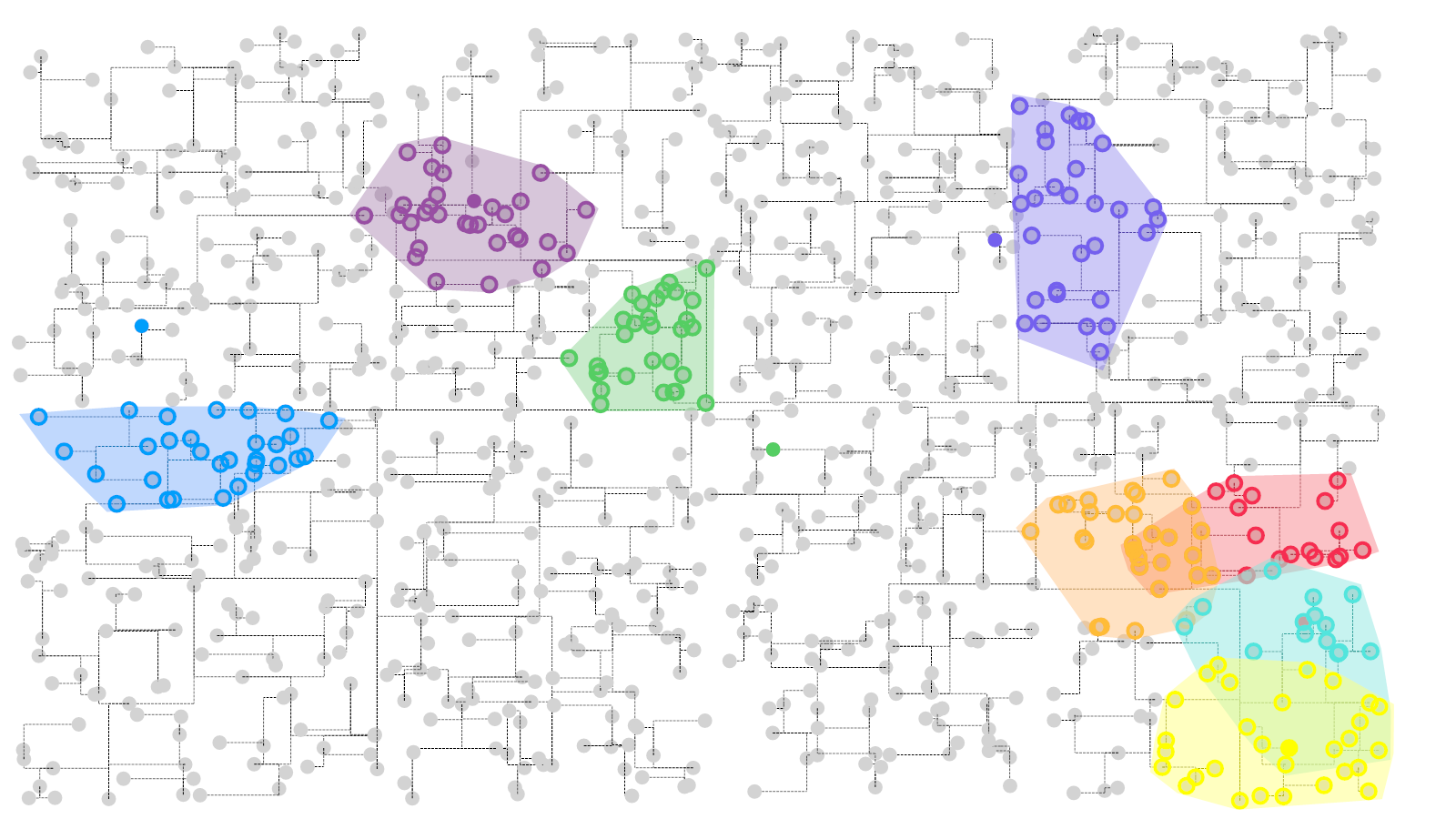
估计阅读时长: 8 分钟https://github.com/xieguigang/sciBASIC 在进行无监督聚类分析的方法之中,我们在算法代码之中一般会遇到求解与某一个样本数据点最相似的数据点的计算过程。对于这个计算过程,一般而言我们是基于欧几里得距离来完成的。 Order by Date Name Attachments Visual a KDtree Search • 274 kB • 343 […]
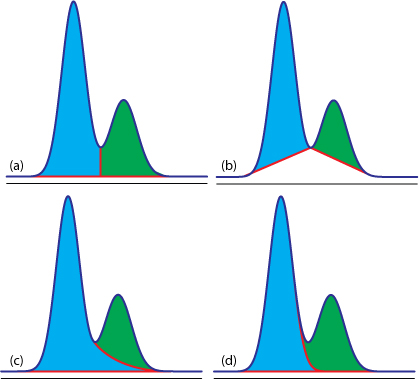
估计阅读时长: 8 分钟https://github.com/xieguigang/sciBASIC/tree/master/Data_science/Mathematica/SignalProcessing 进行峰识别是在代谢组学原始数据分析之中进行定量分析的很重要的一环。在代谢组学之中,定量分析分为靶向定量,以及非靶向定量计算这两大部分。 Order by Date Name Attachments Figure12.36 • 50 kB • 300 click 2021年7月10日view_signal • […]
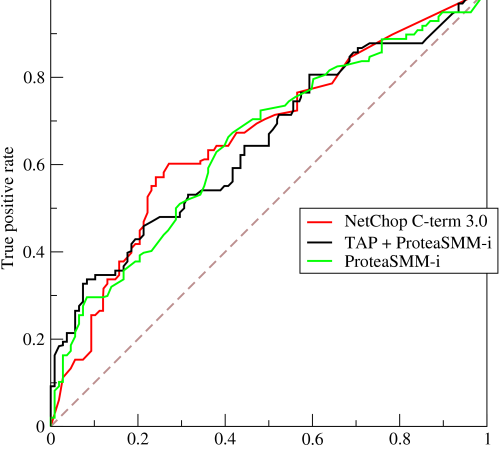
估计阅读时长: 8 分钟https://github.com/rsharp-lang/R-sharp 对于0,1两类分类问题,一些分类器得到的结果往往不是0,1这样的标签。如神经网络得到诸如0.5,0.8这样的分类结果。这时,我们人为取一个阈值,比如0.4,那么小于0.4的归为0类,大于等于0.4的归为1类,可以得到一个分类结果。同样,这个阈值我们可以取0.1或0.2等等。 Order by Date Name Attachments ROC • 221 kB • 344 click 2021年6月28日Roccurves • […]
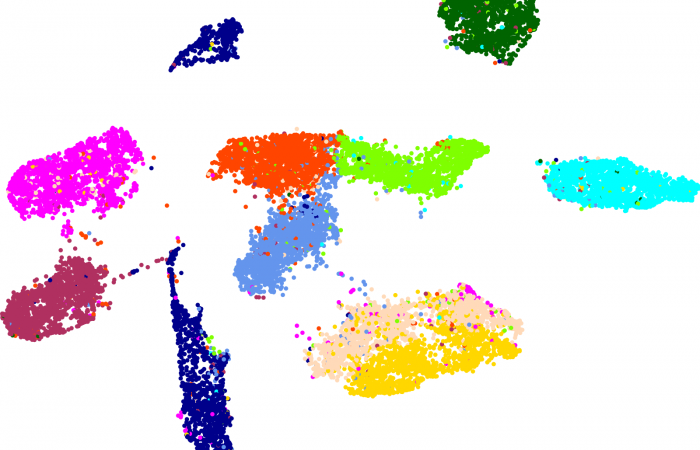
估计阅读时长: 23 分钟https://github.com/rsharp-lang/R-sharp 降维是将数据由高维约减到低维的过程而用来揭示数据的本质低维结构。它作为克服“维数灾难”的途径在这些相关领域中扮演着重要的角色。在过去的几十年里,有大量的降维方法被不断地提出并被深入研究,其中常用的包括传统的降维算法如PCA和MDS;流形学习算法如UMAP、t-SNE、ISOMAP、LE以及LTSA等。 Order by Date Name Attachments MNIST-LabelledVectorArray-60000x100 • 230 kB • 434 click 2021年6月27日MNIST-LabelledVectorArray-60000x100Euclidean_Distance • […]
估计阅读时长: 13 分钟https://github.com/xieguigang/voyager-1 旅行者一号是一艘由NASA在1977年9月5日发射的宇宙飞船,其只比旅行者2号晚16天发射。旅行者一号除了担负着研究我们的太阳系的任务之外,在这艘飞船之上还搭载着一张我们尝试对外界介绍我们的文明的一张名片为“地球之音”的铜质镀金激光唱片,这张金唱片承载着人类与宇宙星系沟通的使命。 Order by Date Name Attachments 1080px-The_Sounds_of_Earth_Record_Cover_-_GPN-2000-001978 • 330 kB • 320 click 2021年6月18日scripting • […]
估计阅读时长: 6 分钟今天在这里和大家聊一下《生物化学系统的计算分析》这本书,生物化学系统的计算分析这本书可以说得上是我的生物信息学学习生涯的启蒙书。 Order by Date Name Attachments Computational Analysis of Biochemical Systems • 875 kB • 230 […]
估计阅读时长: 10 分钟https://github.com/xieguigang/sciBASIC 根据积分表达式,微分方程的数值解关键在于微分方程的初值及计算微分方程式在tm(上一时刻)与tm+d(下一时刻)与坐标轴围成面积,若这个面积计算得越准确则得到的数值解也就越精确。微分表达式中与坐标轴围成的面积可表示如下,在实施算法的时候可以结合这个图更加直观点: 从上面的示意图可以看出,一段需要进行面积积分的曲线实际上是由多个梯形构成的多边形。那我们实际上只需要将这些梯形的面积都求出来,然后加起来就好了。 这里的梯形分割就是一种欧拉逼近的思想,欧拉逼近的几何意义,就是我们可以使用一段折线来近似的逼近一条曲线。 利用欧拉逼近,我们可以将一个精确的微分方程曲线 近似的使用线段来表示 Order by Date Name Attachments ODE_Trapezoidal • 30 kB • […]

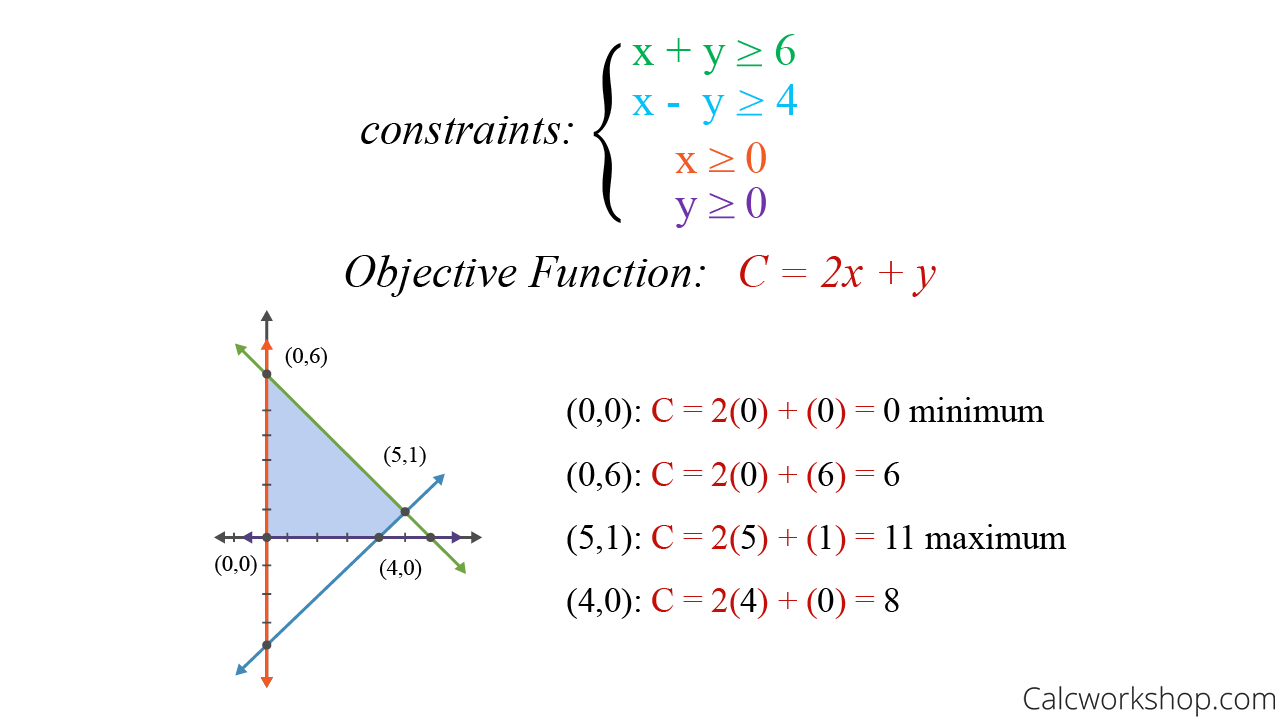



Hello There. I found your website through the usage of msn. This is a very smartly written article. I will…
[…] […]
[…] […]
[…] 《为大语言模型运行添加工具调用》 […]
[…] 《从头创建一个DeepSeek客户端》 […]