R#语言使用龙格库塔法求解劳伦兹混沌系统

https://github.com/xieguigang/sciBASIC

根据积分表达式，微分方程的数值解关键在于微分方程的初值及计算微分方程式在tm(上一时刻)与tm+d（下一时刻）与坐标轴围成面积，若这个面积计算得越准确则得到的数值解也就越精确。微分表达式中与坐标轴围成的面积可表示如下，在实施算法的时候可以结合这个图更加直观点：

从上面的示意图可以看出，一段需要进行面积积分的曲线实际上是由多个梯形构成的多边形。那我们实际上只需要将这些梯形的面积都求出来，然后加起来就好了。

这里的梯形分割就是一种欧拉逼近的思想，欧拉逼近的几何意义，就是我们可以使用一段折线来近似的逼近一条曲线。

利用欧拉逼近，我们可以将一个精确的微分方程曲线

近似的使用线段来表示

但是用梯形面积的和来求解数值解，会存在一个精度问题：例如，如果你观察上图的梯形的顶端与曲线的交接的部分，会发现有空隙。这个空隙就导致了使用梯形面积求解的误差的产生。理论上我们只需要将横坐标轴无限分割，这样子梯形顶端与曲线的空隙就会无限接近于零。但是因为目前计算机精度和算力的限制，我们没有办法做到无限分割。

那有更好的方法来求解积分么？

龙格库塔法求解微分方程

虽然目前我们无法做到无限分割，求取得到最精确的解；但是好在我们可以通过应用改进的欧拉逼近4阶龙格库塔法来进行较为精确的常微分方程组的求解。

下面所示的代码为实现4阶龙格库塔法的伪代码

y(tm + 1) = y(tm) + (k1 + 2 k2 + 2 k3 + k4) / 6 * h   # (1)
k1 = f(y(tm), tm)                                     # (2)
k2 = f(y(tm) + k1 / 2 * h, tm + h / 2)                # (3)
k3 = f(y(tm) + k2 / 2 * h, tm + h / 2)                # (4)
k4 = f(y(tm) + k3     * h, tm + h)                    # (5)

在上面的计算公式中，y(tm + 1)表示下一时刻的数值解，y(tm)表示上一时刻数值解，f()表示微分方程表达式

请注意，y在这里是一个编程语言概念上的数组，所以下一个时刻的数值解是数组的下一个元素T+1，其等价于数学分析上的T+d

龙格库塔法的主要思想：在 Tm 点的附近选取一些特定的点，然后把这些点的函数值进行线性组合，使用组合值代替泰勒展开中 Tm 点的导数值。在上面的伪代码公式中：

• k1 * h 是对阴影面积的一个逼近，欧拉似逼近。
• k2 h 亦是对阴影面积的一个逼近，k1 / 2 h表示用欧拉法求得的是从当前时刻算起跨步长为h / 2的面积，则y(tm)  + k1 / 2 h表示在 tm + h/2处的数值近似解，则k2代表微分表达式tm + h / 2处的值，则2k2 h表示计算了阴影面积的两倍。
• k3 h 更是对阴影面积的逼近，而且比k2 h更为准确，因为k2 h基于欧拉法求得原函数在tm + h / 2处的值从而得到微分表达式在tm + h / 2处的值，k3也是微分表达式在tm + h / 2处的值，只是基于k2，更加精确。2k3 h表示2倍的阴影面积。
• k4 h是对阴影面积的一个逼近，采用y(tm) + h k3得到原函数tm+1时刻的数值解从而求得k4 = f( y(tm) + h k3, tm + h)  为微分表达式在tm + h时刻的解。则k4 h是表示用tm+1时刻的微分表达式值求得的阴影部分面积，也是用矩阵法求得的，属欧拉法。

https://blog.csdn.net/misskissc/article/details/8913941

二阶龙格-库塔法中，泰勒展开到了τ阶，通过与泰勒展开系数进行对比，可以得到含3个未知数的2个方程。依次类推，如果泰勒展开到了 τ^p-1 阶，可以得到 m 级 p 阶龙格-库塔法。

我们将上面的伪代码公式改写为具体的VisualBasic代码，代码如下：

''' <summary>
''' 四阶龙格库塔法解解微分方程，分块数量为n, 解的区间为[a,b], 解向量为(x,y),方程初值为(x0, y0)
''' 参考http://blog.sina.com.cn/s/blog_698c6a6f0100lp4x.html 和维基百科
''' </summary>
''' <param name="df"></param>
''' <param name="n"></param>
''' <param name="a"></param>
''' <param name="b"></param>
<Extension>
Public Sub RK4(ByRef df As ODE, n As Integer, a As Double, b As Double)
    Dim h As Double = (b - a) / n

    df.x = New Double(n - 1) {}
    df.y = New Double(n - 1) {}
    df.x(Scan0) = a
    df.y(Scan0) = df.y0

    Dim x = df.x, y = df.y
    Dim k1, k2, k3, k4 As Double

    For i As Integer = 1 To n - 1
        x(i) = a + h * i
        k1 = df(x(i - 1), y(i - 1))
        k2 = df(x(i - 1) + 0.5 * h, y(i - 1) + 0.5 * h * k1)
        k3 = df(x(i - 1) + 0.5 * h, y(i - 1) + 0.5 * h * k2)
        k4 = df(x(i - 1) + h, y(i - 1) + h * k3)
        y(i) = y(i - 1) + h / 6 * (k1 + 2 * k2 + 2 * k3 + k4)
    Next
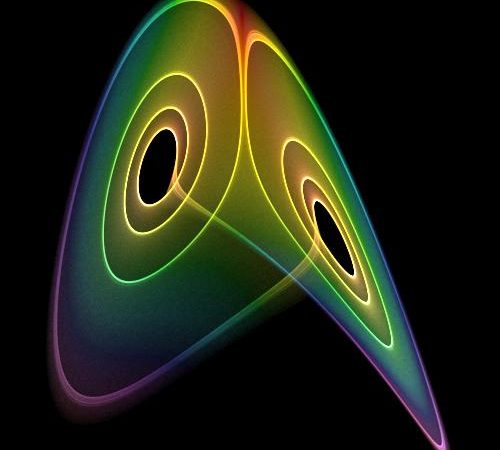
End Sub

利用龙格库塔法求解劳伦兹混沌系统

1963年，Lorenz发现了第一个混沌吸引子——Lorenz系统，从此揭开了混沌研究的序幕，该系统也称为Lorenz混沌系统。Lorenz系统是数值试验中最早发现的呈现混沌运动的耗散系统，其状态方程为：

按照上面的劳伦兹方程，我们可以用R#脚本定义如下所示的常微分方程组进行模拟分析：

require(grDevices3D);
require(charts);

const sigma = 10;
const rho   = 28;
const beta  = 8 / 3;

# define the Lorenz system, and then run runge kutta 4
# via deSolve function.
const lorenz = [
    x -> sigma * (y - x),
    y -> x * (rho - z) - y,
    z -> x * y - beta * z
]
|> deSolve(
    y0 = list(x = 1, y = 1, z = 1),
    a  = 0,
    b  = 10
)
;

# export result as table
lorenz
|> as.data.frame
|> write.csv(file = `${dirname(@script)}/lorenz.csv`)
;

# and then do simple data visualization
bitmap(file = `${dirname(@script)}/lorenz.png`) {
    const view = camera(viewAngle = [30, 30, 30]);

    lorenz
    |> plot(
        vector = list(x = "x", y = "y", z = "z" ),
        camera = view,
        color  = "brown"
    )
    ;
}

在上面的示例代码中，我们的混沌动力学系统使用三个R#语言之中的lambda函数来表示。在设定好了对应常数和系统的初始状态后，将所有的对象都送入到deSolve函数中执行。对上面的常微分方程组通过4阶的龙格库塔法进行数值求解，对结果进行简单的作图可视化之后：

• Author
• Recent Posts

谢桂纲

高级数据科学家 at 苏州帕诺米克

Working on Engineered bacteria CAD design on its genome from scratch. Writing scientific computing software for Tianhe & Sunway TaihuLight supercomputer. Do scientific computing programming in R/R# language, he is also the programming language designer of the R# language on the .NET runtime.

Latest posts by 谢桂纲 (see all)

• 【MZKit】简单自动化组织分区 - 2023年11月5日
• 【MZKit教程】质谱成像原始数据文件查看 - 2023年6月29日
• 生物序列图嵌入算法 - 2023年6月29日