【统计检验】ANOVA检验的代码实现

一般而言，如果我们在进行组学数据分析的时候，如果想要比较两组数据之间是否存在有差异性，一般是对两两比较的两组数据进行T-检验。但是在代谢组学数据分析领域内，则很多的组学数据分析情况为比较两组以上的数据，寻找差异的biomarker。那这个时候就需要使用上ANOVA统计检验方法了。

在讲解ANOVA统计检验方法之前，我们会首先需要来了解F检验。为什么会需要先学习F检验，这是因为ANOVA检验是基于F检验的基础上来完成的。

F检验

F检验也可以称为方差齐性检验。它是一种在零假设（null hypothesis, H0）之下，统计值服从F-分布的检验。其通常是用来分析用了超过一个参数的统计模型，以判断该模型中的全部或一部分参数是否适合用来估计母体。F检验的实现非常的简单：我们将两个待检验的向量的方差相除即可得到F统计值。然后再通过得到的F统计值结果，基于两个向量的自由度进行查表操作既可以得到对应的F检验的Pvalue了。

通过查表得到的Pvalue为单尾检验的Pvalue结果，正常情况下，我们进行F检验一般为双尾检验：即验证两个样本数据的分布是否一致。所以最终的Pvalue值需要在单尾检验的Pvalue值的基础上乘以2得到双尾检验的Pvalue结果。

Public ReadOnly Property F As Double
    Get
        Dim q As Double = XVariance ^ 2
        Dim p As Double = YVariance ^ 2
        Return q / p
    End Get
End Property

Public ReadOnly Property SingleTailedPval As Double
    Get
        Dim f As Double = Me.F
        Dim single_tailed_pval As Double = Distribution.FDistribution(
            fValue:=f,
            freedom1:=XdegreeOfFreedom,
            freedom2:=YdegreeOfFreedom
        )
        Return single_tailed_pval
    End Get
End Property

Public ReadOnly Property PValue As Double
    Get
        Return SingleTailedPval * 2
    End Get
End Property

根据F检验的定义，我们可以简单的实现一下对应的统计方法；然后在R#环境之中测试一下，Pvalue结果值是和R语言之中的F检验结果是一致的。

具体的检验算法实现的源代码，大家可以上Github阅读F检验的源代码文件：FTest.vb

对于具体的F检验计算的应用，最常见的就是在进行t-检验之前我们会需要进行方差齐性检验来判断是否可以使用参数检验，这个方差齐性的判断就是基于F检验的结果来完成的。对于F检验，其还有另一个比较常见的用途，就是在群体遗传学之中做遗传特征的统计分析等。

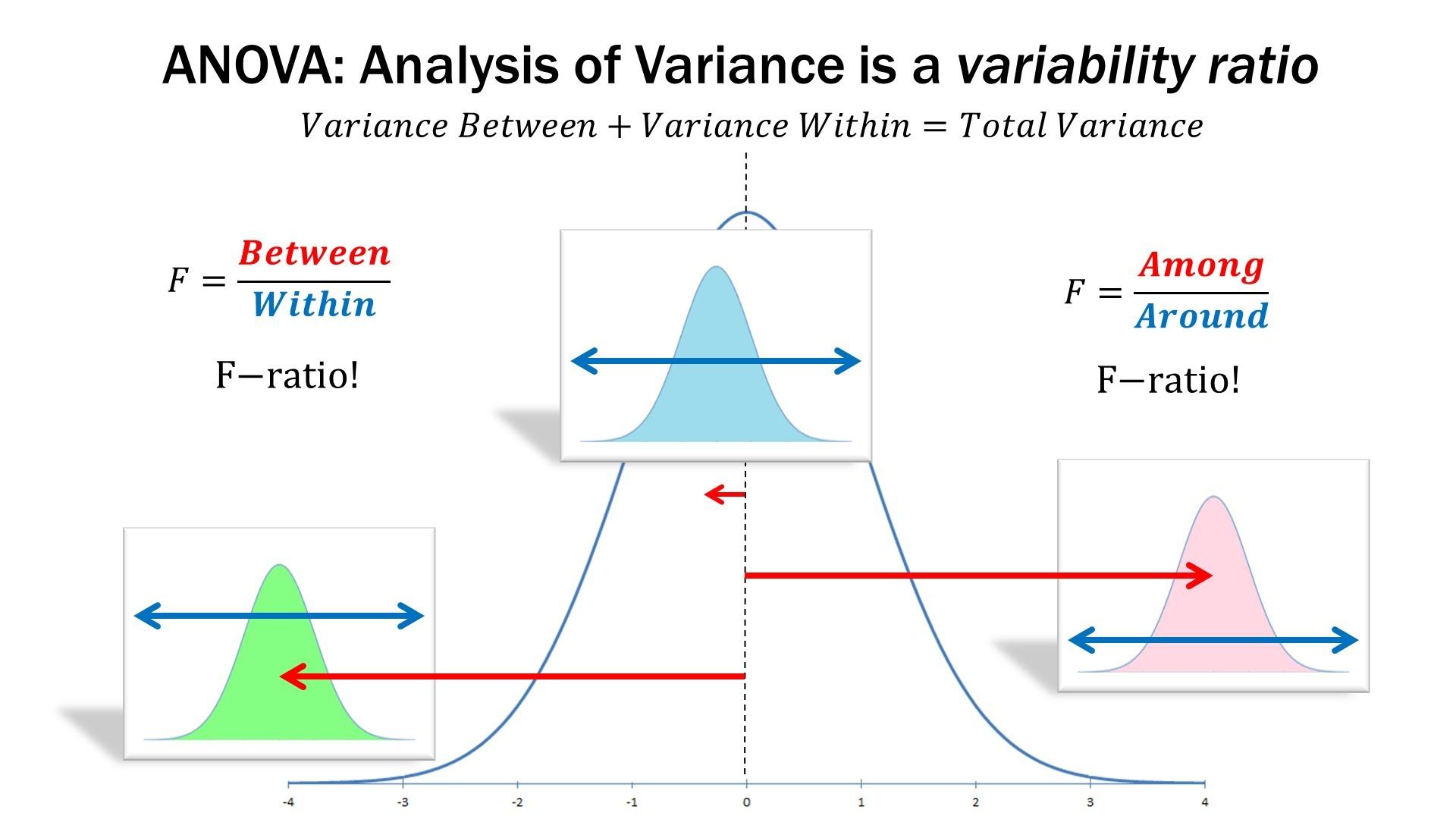
ANOVA检验

上面的公式为ANOVA检验的统计值的计算函数。我们现在将上面的公式和F-检验的统计值计算公式相比较，可以发现，二者是几乎一模一样的。是的，F-test也还可以称为ANOVA(Analysis of Variance)检验。ANOVA检验是用来检测一个y下的不同level的x (也就是组别)下的差异。y是连续变量，x是离散变量，比如类别1，类别2，类别3。那根据具体用途的描述，我们就可以得出ANOVA检验计算的统计学假设为：

H0: μ1 = μ2 = μ3 ... = μk
H1: Means are not all equal.

在ANOVA检验之中，原假设H0为所有因素下的样本数据的方差都是一样的。基于此假设理论，在一般的组学数据分析之中，我们就可以基于ANOVA检验分析来做多组比较。在组学数据分析之中，Feature在不同样本中的表达量就是对应的Y值，相应的level就是我们的实验组别。在做ANOVA分析的时候，我们会需要将不同组别的数据，组装在一块，构成ANOVA的输入进行统计分析：

observations = data.frame(
    v     = [
        2, 3, 7, 2, 6, 
        10, 8, 7, 5, 10, 10, 8, 7, 5, 10, 
        2, 3, 7, 2, 6
    ], 
    group = append(rep("A", 5), append(rep("B", 10), rep("C", 5)))
);

组内平均值计算

在进行实际的ANOVA计算的时候，我们得到的组别结果数据，一般会首先进行组内部的均值的计算，下面的代码展示了组内的均值计算过程：

Dim total As Double = 0
Dim observationsCount = 0

For i As Integer = 0 To groups.Count - 1
    Dim g = groups(i)
    Dim groupTotal As Double = 0

    For j As Integer = 0 To g.ary.Length - 1
        groupTotal += g.ary(j)
    Next

    total += groupTotal
    observationsCount += g.ary.Length
    g.mean = groupTotal / g.ary.Length
Next

allObservationsMean = total / observationsCount

组内方差计算

在上一步完成的组内均值计算之后，我们可以将每一组的平均值赋值给了每个组别的mean字段。接着我们就可以基于这个mean字段平均值结果，进行每组数据的方差计算分析了：

For i As Integer = 0 To groups.Count - 1
    Dim g As Group = groups(i)

    For j As Integer = 0 To g.ary.Length - 1
        Dim observation = g.ary(j)
        Dim result = observation - g.mean
        Dim answer = stdNum.Pow(result, 2)

        g.raisedSum += answer
    Next

    SSW_sum_of_squares_within_groups += g.raisedSum
Next

总方差计算

在前面的计算步骤最开始的组内均值计算过程之中，除了计算出了组内的均值结果，我们还计算出了总体样本的均值结果(allObservationsMean)。那现在基于这个总体样本的均值计算结果，我们就可以计算出总体样本的方差结果数据了：

SS_total_sum_of_squares = 0

For i As Integer = 0 To groups.Count - 1
    Dim g As Group = groups(i)

    For j As Integer = 0 To g.ary.Length - 1
        Dim observation = g.ary(j)
        Dim result = observation - allObservationsMean

        SS_total_sum_of_squares += stdNum.Pow(result, 2)
    Next
Next

SSB_sum_of_squares_between_groups = SS_total_sum_of_squares - SSW_sum_of_squares_within_groups

平均方差计算

现在，基于上面的计算结果之后，我们实际上拿到了组间方差和组内方差的计算结果值，现在我们就会需要根据ANOVA的计算公式，计算出两个平均方差值。然后基于所计算得到的平均方差值，进行F检验计算。

Dim observations = 0

numenator_degrees_of_freedom = groups.Count - 1
SSB = SSB_sum_of_squares_between_groups / numenator_degrees_of_freedom

For Each g In groups
    observations += g.ary.Length
Next

' degrees_of_freedom = observations - groups.size(); 
denomenator_degrees_of_freedom = observations - groups.Count
SSW = SSW_sum_of_squares_within_groups / denomenator_degrees_of_freedom

在上面的计算代码之中，产生了两个用于ANOVA检验所用到的两个很重要的方差计算结果：SSB(Sum of squares between groups)和SSW(Sum of squares within groups)。那现在我们来按照这两个数据对应的计算公式来阅读上面的代码，就可以很清晰的了解到这两个统计值结果是如何产生的了：

• SSB: 这是每组平均值与总平均值之间的平方差的总和乘以每组元素的数量。
• SSW: 这是组均值与组中每个值之间的平方差的总和。

F检验以及P-value计算

当我们通过前面的步骤得到了两个方差统计结果值之后，按照F检验计算的定义，我们就可以按照F检验的统计值计算公式，进行F检验计算了。既然ANOVA方法最终是基于F检验来实现的，那么对应的Pvalue计算是不是也可以同样的通过F分布来完成呢。答案是非常肯定的。在ANOVA计算过程的最后一步，我们在完成了F统计值的计算之后，就可以进行F分布的概率计算：

' anova.fScore_determineIt()
Public Overridable Function fScore_determineIt() As Double
    F_score = SSB / SSW
    singlePvalue = New FDistribution(numenator_degrees_of_freedom, denomenator_degrees_of_freedom).GetCDF(F_score)
    doublePvalue = singlePvalue * 2

    Return F_score
End Function

在计算Pvalue的时候，比较让我惊奇的是，ANOVA检验所使用的是单尾检验Pvalue，而不是常见的双尾检验Pvalue。将我们上面计算得到的单尾pvalue拿出来和R环境之中得到的Pvalue结果比较一下，发现二者一模一样，说明我们的ANOVA检验计算代码是没有问题的。

代码模块测试

分别在RStudio环境中测试R语言的ANOVA以及R#语言环境之中测试自己所编写完成的ANOVA函数，比较二者的结果。可以从下面的测试结果之中看得到，我们所自己编写的ANOVA函数的输出结果与R环境之中的ANOVA计算结果二者保持一致。

observations = data.frame(
    v     = [
        20, 3, 7, 2, 6, 
        10, 8, 7, 5, 10, 10, 8, 7, 5, 10, 
        2,  3, 7, 2, 6
    ], 
    group = append(rep("A", 5), append(rep("B", 10), rep("C", 5)))
);

print(observations, max.print = 6);
#                v    group
# --------------------------
# <mode> <integer> <string>
# [1, ]         20      "A"
# [2, ]          3      "A"
# [3, ]          7      "A"
# [4, ]          2      "A"
# [5, ]          6      "A"
# [6, ]         10      "B"
#
#  [ reached 'max' / getOption("max.print") -- omitted 14 rows ]

test = aov(observations, formula = v ~ group);

str(test);
# List of 16
#  $ Groups degrees of freedom         : int 2
#  $ Observations degrees of freedom   : int 17
#  $ SSW_sum_of_squares_within_groups  : num  267.2
#  $ SSB_sum_of_squares_between_groups : num  56.6
#  $ SSB                               : num  28.3
#  $ SSW                               : num  15.7176
#  $ Residual standard error           : num  3.96455
#  $ SS_total_sum_of_squares           : num  323.8
#  $ allObservationsMean               : num  6.9
#  $ Critical number                   : num  3.4928
#  $ F Score                           : num  1.80052
#  $ Pvalue                            : num  0.195324
#  $ Pvalue(double_tailed)             : num  0.390649
#  $ level                             : chr "p<.05"
#  $ hypothesis                        : chr "The null hypothesis is supported! There is no especial differen"| __truncated__
#  $ summary                           : chr "
# Call:
#    aov(formula = v ~ group, data = observations)
#
# Te"| __truncated__

summary(test);
# Call:
#    aov(formula = v ~ group, data = observations)
#
# Terms:
#                 group Residuals
# Sum of Squares     56.6        267.2
# Deg. of Freedom     2        17
#
# Residual standard error: 3.9645487837613413
# SSB: 28.299999999999926
# SSW: 15.717647058823532
# SS_total_sum_of_squares: 323.7999999999999
# Estimated effects may be unbalanced
# Probability level: p<.05
# allObservationsMean: 6.9
# Critical number: 3.4928
#
# *** F Score:  1.8005239520958034
# *** P-Value:  0.195  [double_tailed: 0.391]
#
# The null hypothesis is supported! There is no especial difference in these groups.

• Author
• Recent Posts

谢桂纲

高级数据科学家 at 苏州帕诺米克

Working on Engineered bacteria CAD design on its genome from scratch. Writing scientific computing software for Tianhe & Sunway TaihuLight supercomputer. Do scientific computing programming in R/R# language, he is also the programming language designer of the R# language on the .NET runtime.

Latest posts by 谢桂纲 (see all)

• 【MZKit】简单自动化组织分区 - 2023年11月5日
• 【MZKit教程】质谱成像原始数据文件查看 - 2023年6月29日
• 生物序列图嵌入算法 - 2023年6月29日