CenterStar多序列比对算法

MSA（多序列比对）在生物信息学中的核心目标是：通过把多条同源序列“对齐”，来突出它们之间的相似与差异，从而帮助我们：识别保守区/功能位点、推断进化关系（系统发生）、预测或解释蛋白质/核酸结构、发现共进化与功能模块，以及为后续分析（如模体搜索、结构建模、从头设计等）提供基础。基于多序列比对分析，我们可以通过这种算法，把一堆表面看上去“乱糟糟”的序列，整理成一个可以“逐位点比较”的框架。基于我们所得到的这个框架基础，我们可以进行下游的后续分析，例如：

1. 识别哪些部分是“不能动”的（功能/结构核心）；
2. 推断它们是如何“进化而来”的（系统发生）；
3. 推测它们在空间中“长什么样”（结构预测与建模）；
4. 找出哪些部分“一起变化”（共进化与功能耦合）；
5. 并把这些信息封装成模型（HMM、profile）用于大规模搜索与注释。

算法的发展历史

多序列比对算法示基于双序列比对算法的基础上发展而来的。基于综述论文“The Historical Evolution and Significance of Multiple Sequence Alignment in Molecular Structure and Function Prediction”(https://www.mdpi.com/2218-273X/14/12/1531)的回顾，于1970年提出来的Needleman–Wunsch 双序列全局最优动态规划算法是整个生物序列比对领域内的鼻祖。

Needleman–Wunsch 算法可以实现对“两条序列”做全局最优比对，通过动态规划得到一个最优得分和比对结果。理论上，我们可以把 Needleman–Wunsch 这种算法推广到多条序列（多维 DP）作比较，但是代价是在时间、空间复杂度上的指数级增加。Needleman–Wunsch算法应用于多序列比对，一般只适用于极短、极少的序列，实际不用于真正的大规模 MSA 。

虽然Needleman–Wunsch算法仅提供了两条序列之间的全局比对结果，但是这个算法为我们今天所讨论的MSA多序列比对算法提供了对应的数学基础。基于最初的序列比对算法的研究，在后面的1987年，提出了Feng–Doolittle 渐进式多序列比对算法 (progressive multiple sequence alignment，https://pmc.ncbi.nlm.nih.gov/articles/PMC287279/），这个算法可以被看做为真正意义上的多序列比对的发展起点的经典算法。

在1990年的时候，Gusfield 等人从算法理论（近似算法、图模型）的角度提出的一条“近似多项式时间”的多序列比对路线(https://www.cambridge.org/core/books/algorithms-on-strings-trees-and-sequences/F0B095049C7E6EF5356F0A26686C20D3)，即center star算法。center star算法于Feng–Doolittle 算法同属于平行发展的两条不同启发式计算算法路线。这两种算法在算法的大框架之上，都是基于利用两两比对结果来构造多序列比对，进行启发式的分布构造多序列比对结果。

Center Star多序列比对原理

我们今天在这里主要进行学习的是center star算法，在所实现的众多多序列对齐算法中，center star算法因为其算法简单，容易进行实现，也是很多的生物信息学课程中大家会首先接触到的算法教程的例子。在center star算法的实现中，这个多序列对齐算法会首先通过两两比较计算，从所有所输入的序列中查找出一条距离其他的任意序列之间距离和最小的一条序列作为中心序列（或者说参考序列），然后在这条找到的参考序列的基础之上，将所有输入的序列都扫描一次，进行两两对齐，即可实现一个渐进似的多序列比对算法。

在多序列比对中，直接计算所有组合的最优解是 NP-Hard 问题。在这里，Center Star 算法采用了一种启发式策略：

1. 这个算法会首先需要选定一条序列作为“中心”。
2. 然后，有了这条参考序列之后，就会将其他所有序列依次与这条中心序列进行双序列比对。
3. 之后，算法会将比对产生的空位“投影”到所有序列上，最终完成多序列比对。

从上面的过程描述中我们可以想象得到，我们首先找到了一条参考序列，然后序列集和中的其他的所有序列都会围绕着这条中心序列进行比对，这个就像是太阳系中的太阳作为中心恒星牵引着其周围所有的行星。故而这里的center star算法这个名称就很形象的描绘出了这个多序列对齐算法的执行过程。

现在，我们假设我们的多序列对齐问题的输入为一个序列集 S = {S1, ..., Sk}, 在这个集合中，每条序列的长读小于等于n，然后我们的算法目标则是输出一个多序列对齐的结果数据集M。基于此，我们现在进行分步骤讲解这个算法的实现过程。

第一步：选择中心序列 (FindStarIndex)

按照上面所描述的第一步，我们会首先需要从输入的序列集合S之中根据一定的规则选择出一条参考序列。在这一步中，我们会对每条序列 St，计算它到所有其它序列的最优比对代价之和（Sum of Pairs, SP分数）：

cost(St) = sum(D(S, St))

在上面的公式中，D(S, St)表示，将我们的序列集合S都和当前的序列St进行一次比较计算，得到编辑距离值，然后对于当前的这条序列St就可以得到他的一个评价结果，与S集合比较的编辑距离值得总和。

Sc = arg min {cost(S1), ..., cost(Sk)}

现在，我们针对S集合中得所有序列都按照上面的计算过程都计算出每一条序列各自所对应得编辑距离值总和之后，取最小值得那条序列，即可得到我们所需要的参考序列，用作为后续多序列对齐操作过程中得中心序列。在下面的函数中，就很清楚的展示了上面的数学计算过程：

''' <summary>
''' This Function finds the minimum star cost from all sequences
''' </summary>
Private Sub FindStarIndex(n As Integer)
    Dim editDists As Integer() = New Integer(n - 1) {}
    Dim k As Integer = Me.kband.K

    Call System.Threading.Tasks.Parallel.For(0, n,
        Sub(i)
            Dim editDist As Integer = 0
            Dim kband As New KBandSearch(globalAlign:=New String(2) {}, k)

            For j As Integer = i + 1 To n - 1
                editDist += kband.CalculateEditDistance(sequence(i), sequence(j))
                editDist += kband.CalculateEditDistance(sequence(j), sequence(i))
            Next

            SyncLock editDists
                editDists(i) = editDist
            End SyncLock
        End Sub)

    ' use the index of min score as the star index
    starIndex = which.Min(editDists)
End Sub

按照上面我们所了解到的定义，中心序列定义为与其他所有序列的编辑距离之和最小的序列。在上面的函数代码中，该方法通过遍历所有序列，计算每一条序列作为中心时的总距离。对于 N 条序列，我们需要计算 N*(N−1)/2 次成对距离，计算量很大。我们为了提升在大型序列数据集上的计算性能，在这里使用了 Parallel.For 进行并行计算，分别计算当前序列与其他所有序列的成对编辑距离之和。最后通过 which.Min 选出距离和最小的序列索引。

第二步：渐进式比对与空位同步 (MultipleAlignment & SyncGaps)

有了中心序列，接下来的工作是“逐个击破”。在下面的所展示的 MultipleAlignment 方法展示了这个过程：

1. 首先，我们会需要一个循环，逐个扫描整个n条序列的序列集合
2. 然后，基于kband比对方法，将中心序列和所扫描的每一条序列进行比对对齐
3. 最后，将当前的比对所产生的空格在所有已经比对过的序列之间进行对齐即可

''' <summary>
''' This function do the multiple alignment according to the center string
''' </summary>
Private Sub MultipleAlignment(n As Integer)
    Dim bar As ProgressBar = Nothing

    ' the center string
    multipleAlign(starIndex) = sequence(starIndex)

    For Each i As Integer In TqdmWrapper.Range(0, n)
        If i = starIndex Then
            Continue For
        Else
            Call bar.SetLabel(names(i))
        End If

        ' 执行双序列比对
        editScores(i) = kband.CalculateEditDistance(multipleAlign(starIndex), sequence(i))
        multipleAlign(i) = kband.globalAlign(1)

        ' 统一处理空格插入，确保所有序列长度一致
        Call SyncGaps(multipleAlign, starIndex, i)
    Next

    Dim maxLen As Integer = Aggregate a As String
                            In multipleAlign
                            Into Max(a.Length)

    For i As Integer = 0 To multipleAlign.Length - 1
        multipleAlign(i) = multipleAlign(i).PadRight(maxLen, GapChar)
    Next
End Sub

阅读代码可以看得到，上面的渐进式多序列对齐函数中，以中心序列multipleAlign(starIndex)为基准，循环将其余序列逐条加入比对。每次迭代中，利用双序列比对算法将当前序列与“当前的中心序列”进行比对。随后调用 SyncGaps 将新产生的空位同步到之前已经比对好的所有序列中，确保多序列长度的一致性。在下面所实现的SyncGaps函数中，会进行空格的查找，然后将查找出来的空格插入到当前已经完成了对齐的序列之中

''' <summary>
''' 同步所有序列的空格插入位置，以新中心序列为基准统一对齐
''' </summary>
''' <param name="alignments">待同步的序列数组</param>
''' <param name="centerIndex">中心序列的索引</param>
''' <param name="i">当前新序列的索引</param>
Private Sub SyncGaps(ByRef alignments As String(), centerIndex As Integer, i As Integer)
    Dim oldCenter As String = alignments(centerIndex)
    Dim newCenter As String = kband.globalAlign(0)
    Dim newSeq As String = kband.globalAlign(1)
    ' 1. 计算旧中心序列到新中心序列的空格插入位置
    '    按位置降序排序，避免插入时索引变动
    Dim gapPositions As Integer() = FindGapInsertPositions(oldCenter, newCenter) _
        .OrderByDescending(Function(p) p) _
        .ToArray

    If gapPositions.Length > 0 Then
        ' 2. 将所有序列（包括新序列）在指定位置插入空格
        Call ApplyGapInsertions(alignments, gapPositions, i)
    End If

    ' 3. 更新中心序列为新比对结果
    alignments(centerIndex) = newCenter
End Sub

''' <summary>
''' 比较新旧中心序列，找出需要插入空格的位置
''' </summary>
Private Shared Iterator Function FindGapInsertPositions(oldCenter As String, newCenter As String) As IEnumerable(Of Integer)
    Dim iOld As Integer = 0
    Dim iNew As Integer = 0

    While iOld < oldCenter.Length AndAlso iNew < newCenter.Length
        If iOld < oldCenter.Length AndAlso oldCenter(iOld) = newCenter(iNew) Then
            ' 字符匹配：移动双指针
            iOld += 1
            iNew += 1
        ElseIf newCenter(iNew) = GapChar Then
            ' 避免在位置0插入gap，防止序列开头出现gap
            If iOld > 0 Then
                Yield iOld
            End If
            iNew += 1
        Else
            ' 字符不匹配：同步移动指针
            iOld += 1
            iNew += 1
        End If
    End While

    ' 处理新中心序列末尾剩余的空格
    While iNew < newCenter.Length
        If newCenter(iNew) = GapChar Then
            ' 在旧序列末尾插入
            Yield iOld
        End If

        iNew += 1
    End While
End Function

''' <summary>
''' 将所有序列在指定位置插入空格（从后向前处理避免索引偏移）
''' </summary>
Private Sub ApplyGapInsertions(alignments As String(), sortedGaps As Integer(), i As Integer)
    ' 只对其他序列（非中心序列）插入gap，保持中心序列固定
    For index As Integer = 0 To i
        ' 跳过中心序列
        If index <> starIndex Then
            Dim sb As New StringBuilder(alignments(index))

            For Each pos As Integer In sortedGaps
                If pos <= sb.Length Then
                    sb.Insert(pos, GapChar)
                Else
                    sb.Append(GapChar)
                End If
            Next

            alignments(index) = sb.ToString()
        End If
    Next
End Sub

在上面所展示的空格处理代码中，首先通过FindGapInsertPositions函数来比较“旧中心序列”和“新中心序列”，找出哪里插入了新的空位。然后，通过 ApplyGapInsertions，我们强制在之前所有的旧序列的相同位置也插入同样的空位。这就好比大家排队，如果排头的人（中心）往前跨了一步，后面所有人都要往前跨一步，保持队形整齐。

K-Band序列比对优化

通过上面的算法代码中我们可以看得到，不管是在最开始的查找中心序列这个步骤中，还是进行渐进式的多序列对齐的步骤中，都会涉及到序列和中心序列之间的两两对齐计算。假若我们没有使用经过优化之后的两两序列全局对齐算法，那么整个多序列对齐的计算过程所花费的时间在处理大型序列数据集上将会是我们无法接受的。

从文章的最起始部分我们了解到，多序列对齐算法是基于Needleman–Wunsch两序列对齐算法的基础上发展而来的。理论上，我们可以直接将Needleman–Wunsch算法应用在上面的center star多序列对齐算法代码之中。但是实际上，直接使用Needleman–Wunsch会导致整个算法的运行时间可能会无法被接受。

所以，为了提升效率，我们在上面所实现的center star算法的底层双序列比对中引入 K-Band 优化，使用kband方法来替换Needleman–Wunsch序列全局对齐算法。标准的 Needleman-Wunsch 算法相比较于K-Band优化算法，其本身时间复杂度是O(L2)。对于生物基因序列，长度可能高达数万，L2的计算太慢了。在这里所实现的K-band优化的两两序列比对算法中，两条相似的序列，其最优比对路径通常不会偏离主对角线太远。我们假设这条路径就在主对角线周围宽度为 K 的带状区域内。在下面所展示的 FillBand 方法中，大家可以看到 j 的范围被限制在 [i-K, i+K] 之间。这意味着我们只计算这一小带状区域内的矩阵格，而忽略远处的格子。这样，复杂度就从 O(L2) 降到了 O(L* K)。当 K 远小于 L 时，速度提升是非常巨大的。

' K-Band 只计算 |i - j| <= K 的区域
' 为了代码简单，我们仍然分配 l1+1 * l2+1 的矩阵，但只更新带内区域
' 如果追求极致空间优化，可以使用偏移量映射的二维数组，但实现较复杂
Dim score(l1, l2) As Integer
Dim trace(l1, l2) As Integer

' 初始化为最大值，表示不可达
For i As Integer = 0 To l1
    For j As Integer = 0 To l2
        score(i, j) = Integer.MaxValue
    Next
Next

' 原点
score(0, 0) = 0

' 初始化边界
' 只有在带内的边界才需要赋值
For i As Integer = 1 To l1
    ' j=0, 必须满足 |i - 0| <= K，即 i <= K
    If i <= K Then
        score(i, 0) = i
        trace(i, 0) = 2 ' Up
    End If
Next

For j As Integer = 1 To l2
    ' i=0, 必须满足 |0 - j| <= K，即 j <= K
    If j <= K Then
        score(0, j) = j
        trace(0, j) = 1 ' Left
    End If
Next

' 填充带状区域
Call FillBand(seq1, seq2, score, trace)

基于动态规划，但引入了K-Band限制。常规DP时间复杂度为 O(L2)，而K-Band假设比对路径偏离主对角线不超过 K，因此仅需计算宽度为 2K+1 的带状区域，将复杂度降低至 O(L⋅K)。

在上面的代码中所调用的Fill Band方法，对于矩阵中的每个单元格 (i,j)，仅当 ∣i−j∣≤K 时才进行计算。计算时检查左、上、左上三个方向的来源，取最小值作为当前得分，并记录回溯路径。

Private Sub FillBand(seq1$, seq2$, ByRef score As Integer(,), ByRef trace As Integer(,))
    Dim l1 = seq1.Length
    Dim l2 = seq2.Length

    For i As Integer = 1 To l1
        ' 确定 j 的范围: [max(1, i-K), min(l2, i+K)]
        Dim jStart As Integer = std.Max(1, i - K)
        Dim jEnd As Integer = std.Min(l2, i + K)

        For j As Integer = jStart To jEnd
            Dim matchCost As Integer = If(seq1(i - 1) = seq2(j - 1), 0, 1)

            ' 计算三个方向的代价，如果来源在带外（值为 MaxValue），则忽略该方向
            ' Diagonal (i-1, j-1)
            ' (i-1) - (j-1) = i - j，所以在带内肯定有效，只要 score 有效
            Dim diagScore As Integer = score(i - 1, j - 1)

            ' Up (i-1, j)
            ' 检查 (i-1) - j 是否在带内 => |(i-1) - j| <= K
            Dim upScore As Integer = Integer.MaxValue
            If std.Abs((i - 1) - j) <= K Then
                upScore = score(i - 1, j)
            End If

            ' Left (i, j-1)
            ' 检查 i - (j-1) 是否在带内 => |i - (j-1)| <= K
            Dim leftScore As Integer = Integer.MaxValue

            If std.Abs(i - (j - 1)) <= K Then
                leftScore = score(i, j - 1)
            End If

            ' 取最小值
            Dim minScore As Integer = diagScore + matchCost
            Dim direction As Integer = 0 ' Diagonal

            If upScore + 1 < minScore Then
                minScore = upScore + 1
                direction = 2 ' Up
            End If
            If leftScore + 1 < minScore Then
                minScore = leftScore + 1
                direction = 1 ' Left
            End If

            score(i, j) = minScore
            trace(i, j) = direction
        Next
    Next
End Sub

然后基于Fill Band方法中所填充得到的trace方向信息，进行对齐过程的回溯：

Dim i As Integer = l1
Dim j As Integer = l2
Dim len As Integer = l1 + l2 ' 最大可能长度
Dim align1(len - 1) As Char
Dim align2(len - 1) As Char
Dim pos As Integer = 0

While i > 0 OrElse j > 0
    Dim t As Integer = trace(i, j)

    If t = 0 Then ' Diagonal
        align1(pos) = seq1(i - 1)
        align2(pos) = seq2(j - 1)
        i -= 1
        j -= 1
    ElseIf t = 1 Then ' Left
        align1(pos) = CenterStar.GapChar
        align2(pos) = seq2(j - 1)
        j -= 1
    ElseIf t = 2 Then ' Up
        align1(pos) = seq1(i - 1)
        align2(pos) = CenterStar.GapChar
        i -= 1
    Else
        ' 不应该发生，除非从错误的地方开始回溯
        Exit While
    End If

    pos += 1
End While

在上面的回溯代码中，代码会从矩阵终点 (l1,l2) 开始，根据记录的路径信息（Trace矩阵）向起点回溯。根据方向决定是输出字符匹配/错配，还是插入空位。最终将反转后的结果作为全局比对字符串输出。

一个小小的DEMO

假设有三条序列{ACGT, ACG, AGT}，首先我们会按照上面的算法流程，选择中心参考序列。在这里算法选择了第三条序列ACT作为参考序列。然后算法流程进入了渐进式的多序列对齐的计算过程。

在渐进式的多序列对齐计算过程中，上面的算法代码会循环逐个扫描序列集合中的每一条序列，分别进行两两对齐：

1. 首先比较序列1：生成了两两序列全局对齐结果 ACT- ~ ACGT
2. 然后是比较序列2：生成了两两序列全局对齐结果 ACT- ~ ACG-
3. 最后比较序列3：是自己比较自己，可以忽略掉

最后生成了下面的比较结果输出：

use [#3]seq_3 sequence as the start center sequence for make alignment!
> seq_name(3) edits MSA Result(cost=406)

        seq_1  1    ACGT
        seq_2  2    ACG-
        seq_3  0    ACT-
                    **

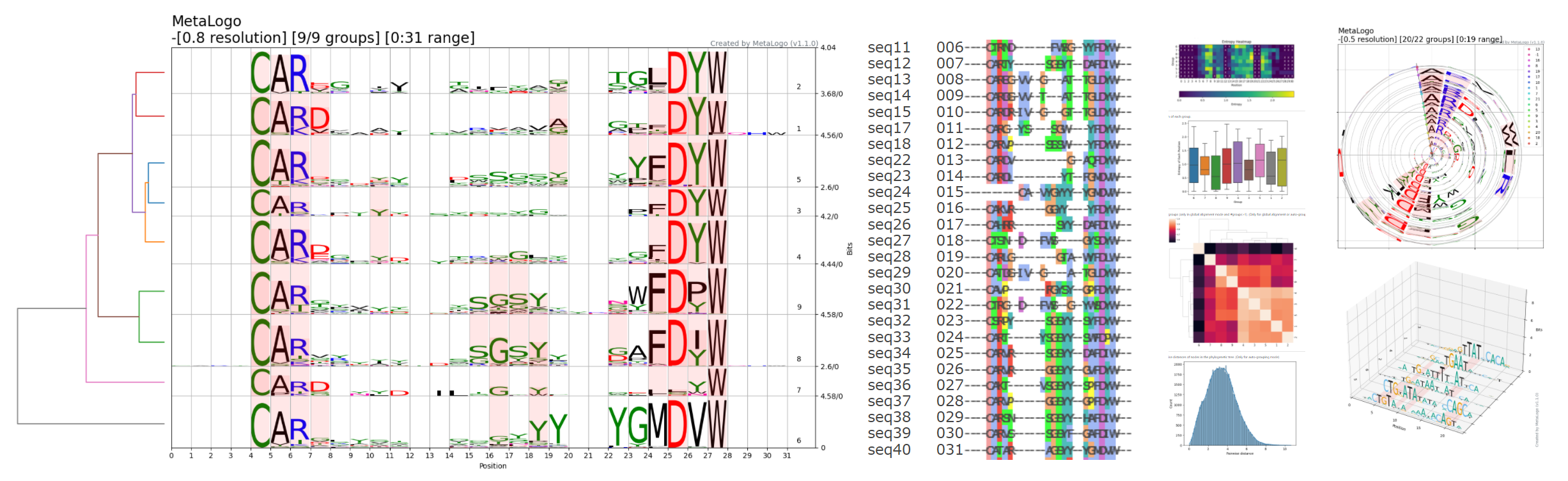
算法测试：多序列比对+SequenceLogo可视化

对上面所示的center star算法代码进行封装后，构建了多序列对齐的MSA函数。基于此，我们编写了下面的脚本代码来进行算法测试：

require(GCModeller);
require(jsonlite);

# Demo script for create sequence logo based on the MSA alignment analysis
# nt base frequency is created based on the MSA alignment operation.

imports "bioseq.patterns" from "seqtoolkit";
imports "bioseq.fasta" from "seqtoolkit";

# read sequence and then do MSA alignment
let msa = MSA.of(read.fasta("seq.fasta"));

print(msa);

# draw sequence logo for make visualization of the 
# MSA result
# by count the nucleotide base frequency
bitmap(file = "logo.png") {
   plot.seqLogo(msa, "LexA");
}

writeLines(jsonlite::toJSON(msa), con = "LexA-MSA.json");

运行上面的测试代码，脚本会首先读取测序所需要的fasta序列数据，然后进行多序列比对。得到多序列比对结果对象之后，会基于对齐后的多序列数据进行每一个位点上的碱基频率的统计，进行sequence logo的绘制，来可视化我们的多序列比对结果。同时，上面的脚本还会将多序列对齐结果导出为json文件，以方便进行下游分析。我们也可以直接在R#环境中查看上面的操作所产生的多序列对齐结果。

按照之前所介绍的《Motif的SequenceLogo图的绘制原理》，对上面的多序列对齐结果进行可视化后，可以得到与gibbs方法产生的motif很相似的可视化结果。

• Author
• Recent Posts

谢桂纲

高级数据科学家 at 苏州帕诺米克

Working on Engineered bacteria CAD design on its genome from scratch. Writing scientific computing software for Tianhe & Sunway TaihuLight supercomputer. Do scientific computing programming in R/R# language, he is also the programming language designer of the R# language on the .NET runtime.

Latest posts by 谢桂纲 (see all)

• 酶EC编号结构解析 - 2026年2月17日
• 二叉树聚类可视化微生物群落代谢差异 - 2026年2月15日
• 通过diamond软件进行blastp搜索 - 2026年2月15日