文章阅读目录大纲
https://github.com/rsharp-lang/ggplot
在进行复杂关系的数据集进行可视化的时候，通过网络图的方式进行数据可视化可以让我们非常直观的借助于网络节点的聚集程度之类的布局信息了解到我们的复杂数据的关系结构信息。最近将R#
网络图的数据结构
对于一个网络图数据模型而言，在整个数据集中主要是通过两种类型的数据构成的：网络边连接以及节点对象。其中节点对象之间通过不同的网络边连接组成一个有机的数据结构，基于一些特定的算法可以根据当前的网络连接结构生成不同的网络节点位置布局。
在网络数据可视化之中，节点对象主要是提供网络节点的一些绘图可视化的元数据，例如节点大小，颜色，形状，标题等。
生成网络模型对象
在R#
require(igraph);
const g = igraph::graph(
from, to, weight,
title = labels,
shape = shapes
);在上面的函数调用结果，我们可以根据from和to边连接集合产生一个网络图对象。同时我们也可以通过weights向量，对对应的序列号的边连接对象设置边连接权重系数。title和shape两个参数则是会需求两个list对象用于分别设置网络图节点的显示标签以及形状等信息。那，现在基于上面所创建的一个基本网络图对象，我们就可以做一些关于网络模型的数据计算操作：
- connected_graph函数将会删除网络中孤立的无任何边连接的节点
- compute.network函数会进行网络节点信息的统计，例如连接度（degree），中介度（betweenness）
- louvain_cluster函数会在当前的网络连接信息以及边连接的权重系数的基础上，基于louvain算法对网络中的节点进行分区，建立网络模块社群
- layout.random最后可以通过随机数，将网络中的节点随机散步在整个网络图之中
require(igraph);
const g = igraph::graph(
from, to, weight,
title = labels,
shape = shapes
)
|> connected_graph()
|> compute.network()
|> louvain_cluster(eps = 1e-100, prefix = "louvain_cluster")
|> layout.random()
;网络可视化
当我们基于上面的代码创建了一个数据信息比较齐全的网络数据模型对象之后，我们就可以基于ggplot程序包做数据可视化了。与普通的ggplot数据可视化过程一样，我们会首先通过ggplot函数加载数据源，然后在数据源的基础上，一层层的往上面叠加图层即可。首先我们创建一个作图的数据源对象：
ggplot(g, padding = "padding: 50px 300px 50px 50px;")在上面的函数之中，g符号为前面所创建的网络图模型对象，padding参数则是用于稍微调整一下我们的网络可视化的画布布局。基于上面的代码所创建的ggplot数据源，接下来我们就可以基于ggraph模块之中的几个主要的函数叠加网络可视化图层了：
- geom_edge_link 函数用于添加网络边连接的图层
- geom_edge_link 函数用于添加网络节点图层
- geom_node_text 函数用于添加网络节点的显示标题文本图层
基于上面的三个ggraph函数做一个基础的网络可视化，我们可以直接进行图层叠加：
ggplot(g, padding = "padding: 50px 300px 50px 50px;")
+ geom_edge_link()
+ geom_node_point()
+ geom_node_text()上面的代码将会创建出一个仅具有最基本的样式的图像可视化结果。很显然，仅有最基本的可视化样式的网络可视化结果肯定不会被我们所满足。所以我们还需要通过上面的几个图层函数的参数做一些绘图样式的微调。例如：
ggplot(g, padding = "padding: 50px 300px 50px 50px;")
+ geom_node_convexHull(aes(class = "group"),
alpha = 0,
stroke.width = 0,
spline = 0,
scale = 1.25
)
+ geom_edge_link(color = "black", width = [1,6])
+ geom_node_point(aes(
size = ggraph::map("degree", [12, 50]),
fill = ggraph::map("group", "paper"),
shape = ggraph::map("shape", pathway = "circle", metabolite = "Diamond")
)
)
+ geom_node_text(aes(size = ggraph::map("degree", [4, 9]), color = "gray"))
;在上面的示例代码之中，geom_edge_link函数可以基于color参数设置网络边连接的线条颜色，width则是可以通过边连接的权重映射设置线条的粗细。geom_node_point函数可以通过aes函数添加一些数据对样式的映射：
- size 基于节点的连接度信息映射节点大小的样式
- fill 则是基于前面通过louvain方法所得到的节点网络社群分组信息映射为不同的颜色
- shape 可以将不同类型分组的网络节点设置为不同的形状，例如pathway类型的节点设置为圆圈，metabolite类型的节点设置为菱形
最后，geom_node_text可以通过aes映射函数将节点的连接度信息映射为文本的字体大小的样式信息。
生成网络布局
如果我们将上面的代码直接绘制出来，尽管网络图通过上面的函数参数调整具有了一定的样式信息，但是节点的布局仍然是前面通过layout.random
在进行网络布局生成的方法之中，最常见的网络布局方法就是力导向图。在ggforce程序包模块之中，提供了一个layout_springforce
layout_springforce(
stiffness = 30000,
repulsion = 100.0,
damping = 0.9,
iterations = 10000,
time_step = 0.0001
)力导向图（Force-Directed layout）
力导向图方法的基本思想为：使用节点间的相似性或距离关系信息作为力，使得相似的节点在空间上接近，同时网络边缘长度相似，并尽可能少的相互交叉。在力导向图之中模拟了物理系统，即假设节点是带电粒子，当它们太靠近时产生排斥力，而边缘的限制充当连接节点的吸引力。
- 优点：节点在区域内均匀分布，并且布局直观，共享更多连接的节点彼此更接近
- 缺点：布局非常慢，计算成本昂贵；
力导向布局的结果往往是一个平衡状态，即使我们试图拖拽一些节点改变网络布局，由于力的存在，网络布局也将会自动恢复。每次布局的结果可能不一致，与设置和点的分布有关。
结果示例
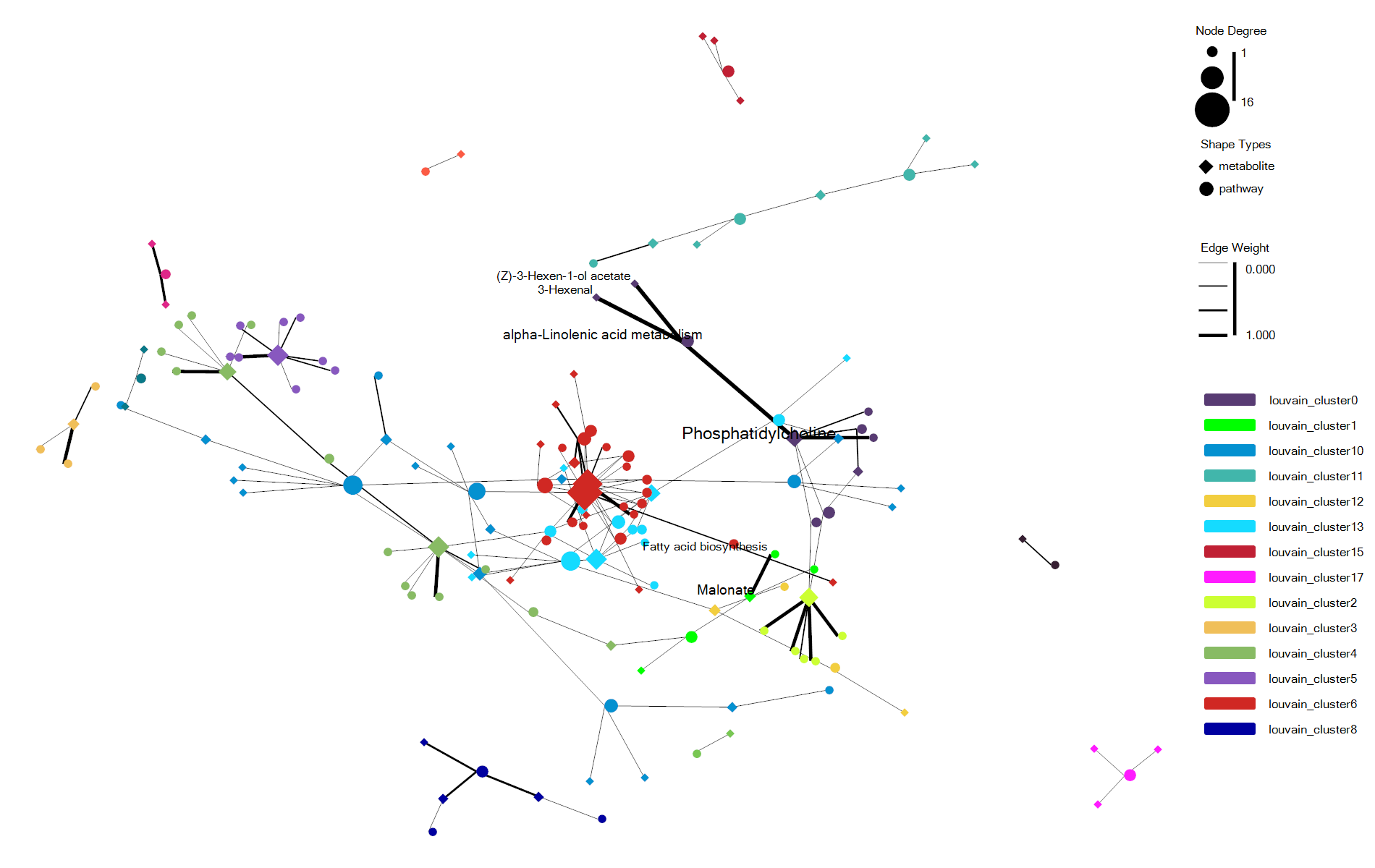
那我们在学习了上面所提到的用于网络可视化所涉及到的函数之后，我们下面来看一个比较完整的ggplot可视化代码例子吧：
ggplot(g, padding = "padding: 50px 300px 50px 50px;")
+ geom_node_convexHull(aes(class = "group"),
alpha = 0,
stroke.width = 0,
spline = 0,
scale = 1.25
)
+ geom_edge_link(color = "black", width = [1,6])
+ geom_node_point(aes(
size = ggraph::map("degree", [12, 50]),
fill = ggraph::map("group", "paper"),
shape = ggraph::map("shape", pathway = "circle", metabolite = "Diamond")
)
)
+ geom_node_text(aes(size = ggraph::map("degree", [4, 9]), color = "gray"), iteration = -5)
+ layout_springforce(
stiffness = 30000,
repulsion = 100.0,
damping = 0.9,
iterations = 10000,
time_step = 0.0001
)
+ theme(legend.text = element_text(
family = "Bookman Old Style",
size = 4
))
;执行上面的ggplot可视化代码之后，我们可以得到与下面类似的网络可视化效果图：
- 【MZKit】简单自动化组织分区 - 2023年11月5日
- 【MZKit教程】质谱成像原始数据文件查看 - 2023年6月29日
- 生物序列图嵌入算法 - 2023年6月29日
No responses yet