文章阅读目录大纲
进行生物化学代谢反应网络的模拟计算,可以分为三种技术路线:基于线性规划做优化的FBA方法,基于常微分方程组求解的动力学模拟方法,以及最近发展的基于图神经网络做模拟计算的深度学习计算方法。在下面的表格中,在这里进行比较和总结了上面所提到的三种计算分析方法各自的计算原理和应用领域:
| 计算方法 | 原理 | 优势 | 适用场景 |
|---|---|---|---|
| 通量平衡分析(FBA) | 基于约束条件(如化学计量矩阵、酶容量限制)和线性规划,在假设代谢网络处于稳态(即代谢物浓度不变)的前提下,计算代谢通量的分布,通常以最大化特定目标(如生物量生长)进行优化 | 1. 无需详细的酶动力学参数,特别适合大规模网络研究。2. 计算速度快,可系统性地预测基因敲除或环境扰动下的表型变化。3. 广泛应用于指导代谢工程,优化目标产物合成。 | 追求快速评估和全局优化:如果你的研究目标是在基因组尺度上快速评估微生物在不同条件下的生长或产物合成潜力,并且难以获取详细的动力学参数,FBA是一个非常实用的起点 |
| 动力学模拟 | 基于质量作用定律等构建常微分方程组(ODEs),描述每个代谢物浓度随时间变化的动力学过程,通过数值方法求解方程组 | 1. 能够捕捉代谢物浓度和通量的瞬态动态变化,揭示更精细的调控机制2. 理论上预测结果准确度更高,能模拟系统偏离稳态时的行为 | 需要研究动态细节和调控机制:如果你关注特定通路在扰动后的精细动态响应、振荡行为或代谢控制分析,并且有或能够测定必要的动力学参数,动力学模拟能提供更深入的见解 |
| 图神经网络(GNN) | 将代谢网络视为图结构(代谢物为节点,反应为边),利用图神经网络等模型学习网络中的复杂拓扑关系和潜在规律,从而对通量等属性进行预测 | 1. 计算效率高,一旦模型训练完成,预测速度极快。 2. 具备强大的表征学习能力,能从数据中挖掘难以手动设计的复杂特征。 3. 对噪声数据表现出较好的鲁棒性 | 处理大量数据并寻求快速预测:当你拥有大量的组学数据或通量数据,并希望建立一个能够快速预测遗传操作或环境变化影响的模型时,基于图神经网络的方法展现出巨大潜力 |
今天在这篇文章中,主要是想讨论下基于常微分方程组对代谢网络做动态求解的方法。首先,我们可以先从《生物化学系统的计算分析》这本书开始进行相关的入门学习,生物化学系统的计算分析这本书可以说得上是我的生物信息学学习生涯的启蒙书。大家可以上Google Books预览这本书。虽然我从后面不断地学习中了解到,其实这本书说的都是系统生物学相关的知识。但是这仍然不妨碍我为了实现相关的系统生物学模拟计算而补充学习其他相关的生物信息学知识。
系统生物学就是对生物系统的计算与数学建模过程。
我到现在任然还记得非常清楚,下面在书中的example2例子开启了我对生命网络系统的仿真模拟的好奇心;并引导了我接下来的,为了通过程序进行自动化构建下面的网络,而不断地补充其他相关的生物信息学知识(例如代谢途径注释,调控网络构建,等)的学习经历,从而诞生了GCModeller这个项目。
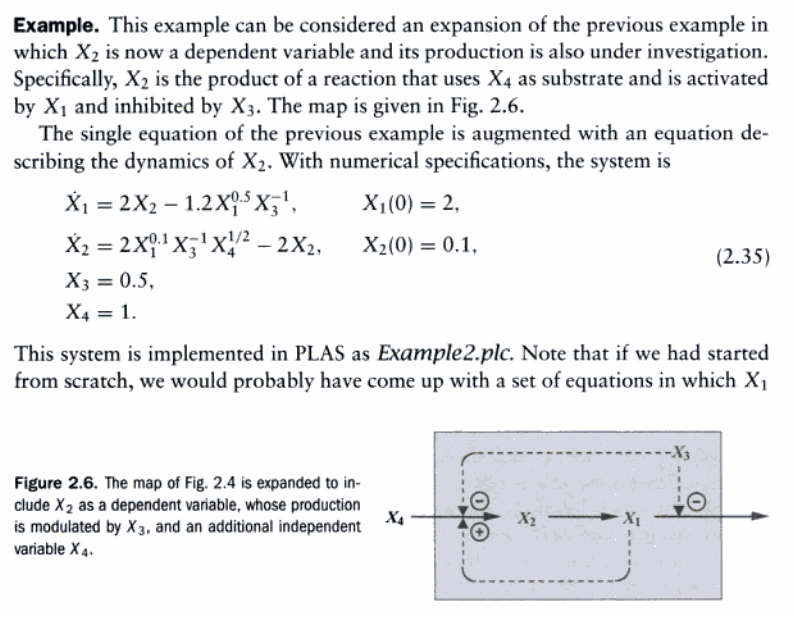

虽然这本书是20多年前出版的一本书,里面的知识相比于目前最新的科研进展可能显得比较陈旧了。但是这本书所介绍的S-system算法我认为是进入系统生物学领域,学习数学建模方面非常经典的一种思想方法。从S-system方程组为入口点来学习生物化学系统的仿真建模的思想,我认为还是非常值得去学习的。为了可以让大家对生物化学系统的仿真建模有一个最基本的认识,我们现在来对于上面的截图中的代谢途径,下面我们来具体的学习以下应该怎么转换为S-system的动力学积分方程。
一般而言在S-system之中,一个变量的浓度变化的动力学过程一般由两部分组成:产生部分以及消耗的部分,也就是一个变量的动力学过程可以有一个通用的表达形式,例如:
# metabolite = SUM(synthesis) - SUM(consumption)
x = a * x1 ^ a1 * x2 ^ a2 * ... - b * x1 ^ b1 * x2 ^ b2 * ...产生的部分为a部分,消耗的部分为b部分。幂指数项ai,bj等则是相应的符号xi与符号x之间的关系。可以看到,
- 如果对应的幂指数项为零,则对应的部分为1,将不会影响乘积结果,即对应的符号与x的变化无关
- 如果对应的幂指数项大于零,则表示催化效应,因为对应的幂的结果总是大于1的
- 反之如果对应的幂指数项小于零,则表示抑制效应。一个符号越大,其负的幂指数结果会越接近于零,整个乘积项将会接近于零,故表现为抑制效应。
所以对于上面的截图中的Figure 2.6的网络示意图,我们可以列出方程:
- x4为净流入,其变化量为一个常数值
- x3同样在系统内为净流入,所以其变化量也是一个常数值
- 对于x2而言,其从x4转换而来,并且转换为x1,所以a部分为x4相关,本部分为其自身降解部分。在x4转换为x2的过程,受x1催化,x3抑制,所以x1的幂指数大于零,x3的幂指数小于零
- 对于x1而言,其来自于x2的转化,并且不受其他因素影响,所以a部分只与x2相关。在消耗部分,因为受到x3的抑制,所以b部分的表达式会与x3相关,并且x3的幂指数小于零
从上面的模型可以看出,x2的消耗的表达式部分与x1的生成的表达式部分是一样的,这个是因为我们的模型要遵守自然界之中最基本的物质守恒定律。
在系统生物学里面,模拟一个动力学系统,实际上就是一个微积分方程组的求解过程。关于使用R#脚本进行动力学系统的模拟计算的原理,我们可以阅读之前写的博客文章:《R#语言使用龙格库塔法求解劳伦兹混沌系统》。
在这里我们仍然是使用lambda函数来表示一个微分方程组,通过这个微分方程组来构建出一个动力学系统:
let network = [
x1 -> 2 * x2 - 1.2 * (x1 ^ 0.5) * (x3 ^ (-1)),
x2 -> 2 * (x1 ^ 0.1) * (x3 ^ (-1)) * (x4 ^ 0.5) - (2 * x2),
x3 -> 0.5,
x4 -> 1
];
network |> deSolve(
y0 = list(
x1 = 2,
x2 = 0.1,
x3 = 0.5,
x4 = 1
),
a = 0,
b = 10,
resolution = 20000
)
|> as.data.frame
|> write.csv(file = "./example2.csv")
;执行上面的脚本求解微分方程组的积分结果,得到的曲线的值和书中的example 2示例的结果相比,比较尴尬,有点不一样。不太清楚是不是积分计算的方法差异或者是计算的分辨率的不同导致的问题:
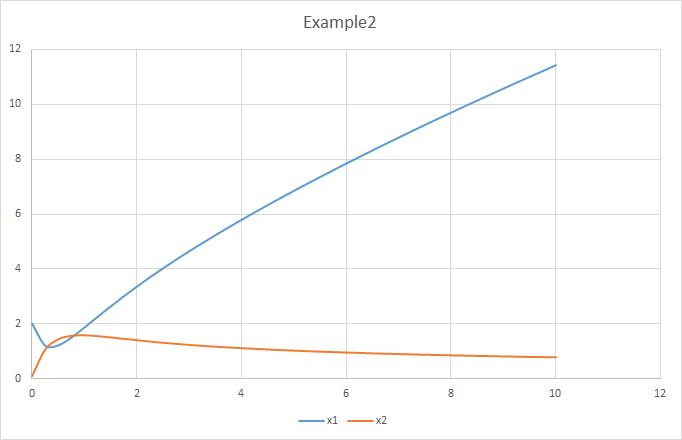
虽然最终的结果值不太一样,但是变化趋势是与书中描述的是一样的:
X1变量首先会因为X3浓度较低,抑制力作用较低而在初期有一个较大的消耗量。在曲线上首先展现出一个被消耗的趋势,之后由于X3浓度不断累积,X1的消耗反应接近停止,X1表现出在后期不断地累积;
X2变量而言,由于其通过X4转化的过程受X3抑制,因为X3后期不断累积,所以X4转化为X2的过程在不断的受抑制,X2的转化效率低于其转化为X1的时候,X2的浓度将会不断降低
通过上面所展示的基于desolve函数进行常微分方程组的求解结果,得到的模拟输出实际上通常为各代谢物浓度随时间变化的数据表或曲线。例如,假设我们对TCA循环做建模模拟分析,通过绘制时间-浓度曲线,可以直观观察TCA循环的动态行为。例如,可绘制柠檬酸、α-酮戊二酸、琥珀酸、苹果酸和草酰乙酸等中间产物的浓度变化曲线。理想情况下,这些曲线应呈现周期性波动,最终趋于稳态。若模型参数合理,模拟曲线应与实验测定趋势一致。
GCModeller之中内置的PLAS计算引擎
在GCModeller的simulators模块之中,定义了一个S.system
在这个程序包模块之中,提供了有一些与生物化学系统建模脚本化编程相关的api:
- snapshot 函数用来打开一个用来进行本地数据存储的文件设备,用来保存模拟器输出的每一帧符号数据,可以从下面的代码看到,这个函数接受一个符号列表用来选择性的输出结果数据
- kernel 函数用来创建一个基于S-system算法的生物化学系统动力学模拟器对象
- environment 函数就是用来配置kernel中的一些符号常量等信息
- s.system 函数就是用来向模拟器核心加载我们所定义的S-system系统方程
- run 最后run函数就是执行整个模拟器的运行
PLAS模拟器脚本示意
下面我展示了demo代码,查看如何通过GCModeller所提供的PLAS系统相关的api来进行动力学系统模拟计算的脚本化编程:
imports "S.system" from "simulators";
# set y0 of the ODEs system
let symbols = list(
x1 = -100,
x2 = -100000,
x3 = 0,
x4 = 10
);
# open data connection for export to a csv table file
using data.driver as snapshot("./atkinson.csv", symbols = names(symbols)) {
data.driver
|> kernel(S.script("Atkinson system"))
|> environment(
beta1 = 30,
beta3 = 30,
beta4 = 1,
lamda1 = 2,
lamda3 = 2,
alpha1 = 20,
alpha2 = 20,
alpha3 = 1,
a = 1,
n1 = 4,
n2 = 5,
n3 = 1,
is.const = TRUE
)
|> environment(symbols)
|> s.system([
x1 -> beta1 * (lamda1 * (1 + alpha1 * (x4 ^ n1) / (1 + x4 ^ n1)) - x1),
x2 -> x1 - x2,
x3 -> beta3 * (lamda3 * (1 + alpha2 * ((x4 / a) ^ n2) / (1 + (x4 / a) ^ n2)) * (1 / (1 + x2 ^ n3)) - x3),
x4 -> beta4 * (x3 - x4)
])
|> run(ticks = 4.5, resolution = 0.1);
}可以看到,执行上面的脚本代码,上面的S-system动力学方程组输出了这样的一个无限震荡并且信号放大的动力学系统。

在最上面开始的时候,我们提到了针对三羧酸循环的模拟计算,那下面我们就以TCA循环为例,来进一步讲解整个模拟计算的过程和方法。
三羧酸循环建模示例
三羧酸循环(Tricarboxylic Acid Cycle, TCA循环),又称柠檬酸循环或Krebs循环,是需氧生物体内将乙酰辅酶A(Acetyl-CoA)彻底氧化为二氧化碳和水,并在此过程中产生还原当量和ATP的核心代谢途径。该循环不仅是细胞能量代谢的枢纽,还为生物合成反应提供关键中间代谢物,因而在细胞生理和病理研究中占据核心地位。通过数学模型对TCA循环进行模拟,可以定量预测代谢物浓度随时间的变化,揭示调控机制,并为代谢工程和疾病研究提供理论依据。

TCA循环包含8个关键酶促反应,涉及多种代谢中间物。经典TCA循环从草酰乙酸(Acetyl-CoA)与草酰乙酸(Oxaloacetate,4碳)缩合形成柠檬酸(6碳)开始,经多步氧化脱羧最终再生草酰乙酸,完成循环。主要反应步骤包括:
- 柠檬酸合成(Citrate Synthesis):草酰乙酸 + 草酰乙酸 → 柠檬酸(由柠檬酸合酶催化,该反应为限速步骤之一)。
- 异构化(Aconitase Reaction):柠檬酸 → 异柠檬酸(由顺乌头酸酶催化,经脱水-加水步骤)。
- 氧化脱羧(Isocitrate Dehydrogenation):异柠檬酸 + NAD⁺ → α-酮戊二酸 + CO₂ + NADH(由异柠檬酸脱氢酶催化)。
- 再次脱羧(α-Ketoglutarate Dehydrogenation):α-酮戊二酸 + NAD⁺ + CoA-SH → 琥珀酰辅酶A + CO₂ + NADH(由α-酮戊二酸脱氢酶复合体催化)。
- 底物磷酸化(Succinyl-CoA Synthetase):琥珀酰辅酶A + Pi + GDP → 琥珀酸 + GTP + CoA-SH(由琥珀酰辅酶A合成酶催化)。
- 琥珀酸脱氢(Succinate Dehydrogenation):琥珀酸 + FAD → 延胡索酸 + FADH₂(由琥珀酸脱氢酶催化,该酶嵌入线粒体内膜)。
- 延胡索酸水合(Fumarase):延胡索酸 + H₂O → 苹果酸(由延胡索酸酶催化)。
- 苹果酸脱氢(Malate Dehydrogenation):苹果酸 + NAD⁺ → 草酰乙酸 + NADH(由苹果酸脱氢酶催化)。
上述反应构成一个循环网络,其中中间代谢物(如柠檬酸、α-酮戊二酸、琥珀酸、延胡索酸、苹果酸等)的浓度随时间变化,驱动整个循环的运转。建模的目标就是用数学方程描述这些代谢物浓度随时间的变化规律。为了便于进行演示,我们在这里对上面的TCA循环网络分解为如下的网络中所涉及到的每一个化合物其各自所设计的合成和消耗部分的信息表格:
| Metabolite | Synthesis | Consumption |
|---|---|---|
| Acetyl-CoA | NA | (Oxaloacetate + Acetyl-CoA) |
| CO₂ | (Isocitrate + NAD⁺) (α-Ketoglutarate + NAD⁺ + CoA-SH) | NA |
| Citrate | (Oxaloacetate + Acetyl-CoA) | (Citrate) |
| CoA-SH | (Succinyl-CoA + Pi + GDP) | (α-Ketoglutarate + NAD⁺ + CoA-SH) |
| FAD | NA | (Succinate + FAD) |
| FADH₂ | (Succinate + FAD) | NA |
| Fumarate | (Succinate + FAD) | (Fumarate + H₂O) |
| GDP | NA | (Succinyl-CoA + Pi + GDP) |
| GTP | (Succinyl-CoA + Pi + GDP) | NA |
| H₂O | NA | (Fumarate + H₂O) |
| Isocitrate | (Citrate) | (Isocitrate + NAD⁺) |
| L-Malate | (Fumarate + H₂O) | (L-Malate + NAD⁺) |
| NAD⁺ | NA | (Isocitrate + NAD⁺) (α-Ketoglutarate + NAD⁺ + CoA-SH) (L-Malate + NAD⁺) |
| NADH | (Isocitrate + NAD⁺) (α-Ketoglutarate + NAD⁺ + CoA-SH) (L-Malate + NAD⁺) | NA |
| Oxaloacetate | (L-Malate + NAD⁺) | (Oxaloacetate + Acetyl-CoA) |
| Pi | NA | (Succinyl-CoA + Pi + GDP) |
| Succinate | (Succinyl-CoA + Pi + GDP) | (Succinate + FAD) |
| Succinyl-CoA | (α-Ketoglutarate + NAD⁺ + CoA-SH) | (Succinyl-CoA + Pi + GDP) |
| α-Ketoglutarate | (Isocitrate + NAD⁺) | (α-Ketoglutarate + NAD⁺ + CoA-SH) |
在这里,我们提取了反应列表中的所有代谢物名称,并针对每个代谢物,遍历了代谢反应列表,提取了合成对应的方程式右侧信息(即代谢物作为产物时,反应物侧的表达式)作为第二列,以及消耗对应的方程式左侧信息(即代谢物作为反应物时,反应物侧的表达式)作为第三列。在上面的表格中,NA表示没有对应的项目。将循环外部的底物(如Acetyl-CoA)和辅助因子(如NAD⁺、FAD)之类的因素从循环中删除,仅留下循环中的主路径中的化合物。这样子,基于前面所总结出来的S系统通用表达式,我们可以简单的将TCA循环转化为下面的S系统语言:
# Citrate Synthesis: Oxaloacetate + Acetyl-CoA → Citrate
# Isomerization (Aconitase Reaction): Citrate → Isocitrate
# Oxidative Decarboxylation (Isocitrate Dehydrogenation): Isocitrate + NAD⁺ → α-Ketoglutarate + CO₂ + NADH
# Second Decarboxylation (α-Ketoglutarate Dehydrogenation): α-Ketoglutarate + NAD⁺ + CoA-SH → Succinyl-CoA + CO₂ + NADH
# Substrate-Level Phosphorylation (Succinyl-CoA Synthetase): Succinyl-CoA + Pi + GDP → Succinate + GTP + CoA-SH
# Succinate Dehydrogenation: Succinate + FAD → Fumarate + FADH₂
# Fumarate Hydration (Fumarase): Fumarate + H₂O → L-Malate
# Malate Dehydrogenation: L-Malate + NAD⁺ → Oxaloacetate + NADH
let TCA_cycle = [
# metabolite synthesis consumption
citrate -> (oxaloacetate^0.5) - (citrate ^ 0.5),
fumarate -> (succinate ^ 0.5) - (fumarate ^0.5),
isocitrate -> (citrate ^ 0.5) - (isocitrate ^ 0.5),
l_malate -> (fumarate ^0.5) - (l_malate^0.5),
oxaloacetate -> (l_malate^0.5) - (oxaloacetate^0.5),
succinate -> (succinyl_coA ^ 0.5) - (succinate ^ 0.5 ) ,
succinyl_coA -> (a_ketoglutarate ^ 0.5) - (succinyl_coA ^ 0.5),
a_ketoglutarate -> (isocitrate ^ 0.5) - (a_ketoglutarate ^ 0.5)
];按照上面所示例的脚本配置好PLAS计算引擎后,即可开始执行整个循环的动力学模拟计算:
require(GCModeller);
# load PLAS simulator package module
imports "S.system" from "simulators";
let metabolites = list(
citrate = 100, fumarate = 20, isocitrate = 20,
l_malate = 20, oxaloacetate = 20,
succinate = 20, succinyl_coA = 20,
a_ketoglutarate = 20
);
# open data connection for export to a csv table file
using data.driver as snapshot(relative_work("TCA-cycle.csv"), symbols = names(metabolites)) {
data.driver
|> kernel(S.script("TCA cycle"),strict=FALSE)
|> environment(metabolites)
|> s.system(TCA_cycle)
|> run(ticks = 150, resolution = 0.005);
}
从上面的模拟计算结果可以发现,整个循环途径在没有外部物质补充进来的时候,经过最初的震荡之后,TCA循环被驱动起来后,最终系统达到了稳定状态。
- 单细胞视角下的微生物基因组代谢酶嵌入分析 - 2026年2月25日
- 基因组代谢酶层级嵌入 - 2026年2月23日
- 基因组功能吉布斯LDA主题建模 - 2026年2月23日




No responses yet