limma程序包在RNA-seq差异表达分析中的数学算法原理与实现详解

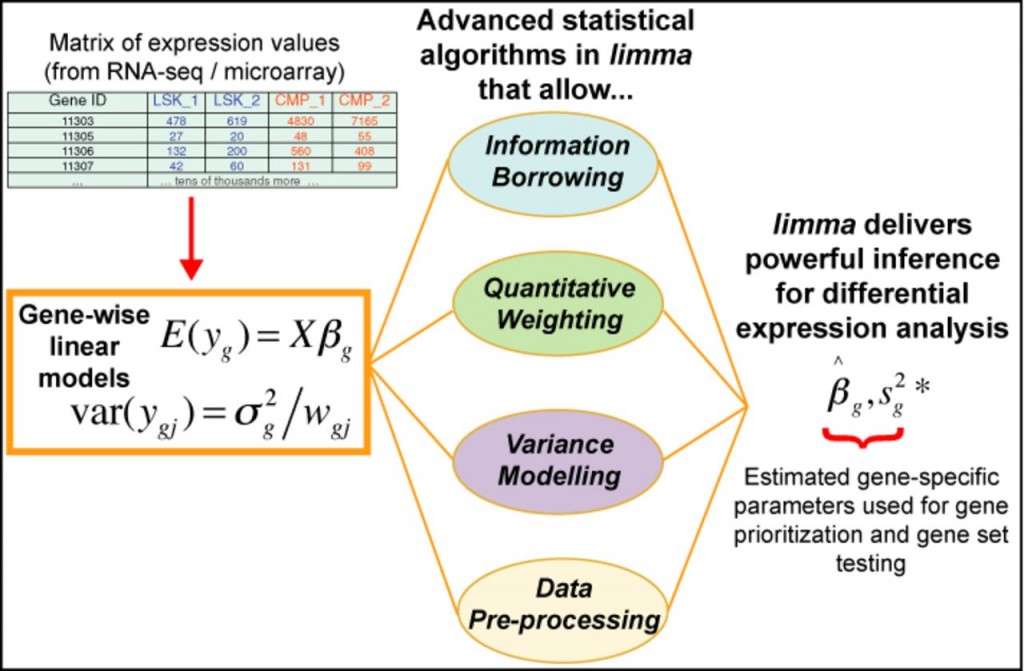
limma（Linear Models for Microarray Data）是一个基于R语言的Bioconductor包，最初用于微阵列数据的差异表达分析，现已扩展支持RNA-seq数据。其核心思想是利用线性模型（Linear Models）对基因表达数据进行建模，并结合经验贝叶斯（Empirical Bayes）方法在小样本情况下增强统计推断的稳健性。

通过limma程序包进行差异表达统计检验计算分析，整体分析流程通常包括以下关键步骤：

1. 数据导入与预处理：读取原始表达数据（对于RNA-seq，通常是基因的read counts矩阵），并进行必要的预处理，如过滤低表达基因、归一化等。limma本身不直接执行原始count的归一化，但提供了与edgeR等包的接口，可以方便地导入经过TMM（Trimmed Mean of M-values）等归一化后的数据。
2. 数据转换与权重计算（voom）：对于RNA-seq的count数据，limma通过voom函数将其转换为适合线性模型分析的形式。voom方法估计每个观测值（基因在样本中的表达值）的均值-方差关系，并据此计算精度权重（precision weights）。这些权重反映了不同观测值的可靠性差异，将被纳入后续的线性模型分析中。经过voom处理后，RNA-seq数据在形式上与微阵列数据类似，从而可以复用limma为微阵列开发的成熟分析流程。
3. 线性模型拟合：对每个基因分别拟合一个线性模型，以解释其表达量在不同实验条件或处理组之间的变异。设计矩阵（design matrix）用于指定实验设计，包括不同处理组、批次效应等协变量。通过最小二乘法（或加权最小二乘，如果提供了权重）估计模型参数，得到每个基因在各组之间的差异表达量（即系数估计）以及残差等统计量。
4. 经验贝叶斯方差估计：由于RNA-seq实验样本量通常较小，直接使用每个基因的样本方差估计进行统计检验会导致检验功效低下且不稳定。limma采用经验贝叶斯方法，将所有基因的方差估计视为来自一个共同的先验分布，从而“借用”跨基因的信息来改进每个基因的方差估计。具体而言，limma假设各基因的残差方差服从逆卡方分布，并利用数据估计先验参数，然后将基因特异性方差向先验均值“收缩”（shrinkage）。这一过程显著提高了小样本情况下方差估计的稳定性，并增大了统计检验的自由度，从而提升检测差异表达基因的统计功效。
5. 差异表达统计推断：在经验贝叶斯调节后的方差基础上，对每个基因的组间差异进行假设检验。limma主要输出经验贝叶斯调节的t统计量（moderated t-statistic）及其对应的P值。此外，还提供经验贝叶斯调节的F统计量（moderated F-statistic）用于同时检验多个 contrasts（例如多个处理组之间是否存在差异）。对于多重假设检验带来的问题，limma支持多种校正方法（如Benjamini-Hochberg FDR）来控制错误发现率。
6. 结果汇总与可视化：使用topTable函数可以方便地提取差异表达分析的结果，包括每个基因的log2倍数变化（logFC）、平均表达量（AveExpr）、t统计量、P值、校正后的P值以及贝叶斯统计量B等。这些结果可以进一步用于功能富集分析、基因集检验等下游分析。limma还提供了丰富的绘图功能（如MA图、火山图、均值-方差趋势图等）帮助用户直观地理解数据和分析结果。

上述流程构成了limma在RNA-seq差异表达分析中的核心框架。接下来，我们将深入探讨其中的数学模型与算法原理，重点解析线性模型拟合、数据标准化、方差估计、t检验与贝叶斯统计推断等关键步骤。

Limma核心算法原理

线性模型与复杂实验设计

limma的核心优势在于其灵活的线性模型框架，能够处理各种复杂的实验设计。对于每个基因，limma拟合一个线性模型来描述其表达量与实验条件之间的关系。以简单的两样本比较为例，假设有n个样本，其中n₁个属于处理组，n₂个属于对照组，第i个样本中某基因的表达量为y_i。线性模型可表示为：

y = beta0 + beta * x + epsilon

其中x_i是表示组别的指示变量（例如对照组取0，处理组取1），β₀是截距（对照组的平均表达水平），β₁是处理效应（处理组相对于对照组的差异），ε_i是随机误差项。该模型等价于对两组均值进行比较，β₁即为两组均值之差（在log2尺度下即为logFC）。

对于更复杂的多因素设计，例如包含多个处理组、时间序列、配对样本或批次效应等，线性模型可以扩展为：

y = X %*% beta + epsilon

其中y是n × 1的响应向量（某基因在各样本中的表达量），X是n × p的设计矩阵，其每一列对应一个协变量（如处理组别、批次、性别等），β是p × 1的系数向量，ε是n × 1的误差向量。设计矩阵X的构造非常灵活，可以包含因子型变量的不同水平、连续变量以及它们的交互作用等，从而实现对任意复杂实验设计的建模。例如，对于一个包含3个处理组的实验，设计矩阵可以包含两个哑变量来表示组别差异；对于配对样本设计，可以引入配对因子作为协变量；对于时间序列数据，可以引入时间变量或时间与处理的交互项等。

通过最小二乘法，可以估计出系数向量βhat，使得残差平方和最小。在普通线性模型中，假设误差ε_i独立同分布，且ε_i ∼ N(0, sigma²)，则βhat的协方差矩阵为sigma²(X^TX)^-1。然而，在基因表达数据中，不同基因的方差sigma²往往不同，且样本量有限导致直接估计每个基因的sigma²不可靠。这正是limma引入经验贝叶斯方法的原因。

经验贝叶斯方差估计与t统计量

在获得标准化的表达数据和设计矩阵后，limma对每个基因拟合线性模型，得到系数估计 β̂_j（例如组间差异）和残差标准差 s。对于第 j 个基因的第 k 个系数（例如某个处理效应），其常规t统计量定义为：

t_ord = beta_jk / (s * sqrt(v_kk))

其中 s_j 是第 j 个基因的残差标准差（基于样本数据估计），v_kk 是设计矩阵 X 的第 k 列对角元素（即 (X^TX)^-1 的第 k 个对角元素），用于调整系数估计的标准误差。常规t统计量服从自由度为 n-p 的t分布（n 为样本数，p 为模型参数个数），可用于检验 β_jk=0 的假设。

然而，当样本量 n 很小时，s_j 的估计非常不稳定，可能导致t统计量的分布偏离理论t分布，从而影响P值的准确性。limma通过经验贝叶斯方法对 s_j 进行收缩（shrinkage）。其核心思想是：假设所有基因的残差方差 s_j² 来自一个共同的先验分布，然后利用数据估计该先验分布的参数，进而得到每个基因方差的后验估计。

具体而言，limma假设 s_j² 服从逆卡方分布（inverse chi-squared distribution），即 s_j² ~ σ₀² χ_d0^-2，其中 σ₀² 和 d₀ 是先验参数（分别表示先验方差和先验自由度）。通过矩估计等方法，limma从所有基因的 s_j² 中估计出 σ₀² 和 d₀。然后，第 j 个基因的后验方差 s_j^2post 可表示为先验方差与样本方差的加权平均：

s_post = (d0 * sigma0_sq + (n-p) * s_sq) / (d0 + (n-p))

这个公式体现了“借用信息”的思想：当样本量 n-p 较小时，s_j² 的权重较小，s_j^2post 更接近先验均值 σ₀²；反之，当 n-p 较大时，s_j^2post 更接近样本估计 s_j²。通过这种收缩，小样本基因的方差估计被“拉向”整体趋势，而大样本基因的方差估计基本保持不变，从而提高了估计的稳定性。

基于后验方差 s_j^post，limma计算经验贝叶斯调节的t统计量（moderated t-statistic）：

t_mod = beta_jk / (s_post * sqrt(v_kk))

与常规t统计量相比，t_jk^mod 使用了经过经验贝叶斯调节的标准误差 s_j^post * sqrt(v_kk)。由于 s_j^post 融合了先验信息，其估计更精确，对应的自由度也增大为 d₀ + (n-p)。因此，t_jk^mod 在零假设下近似服从自由度更高的t分布，这使得在样本量较小时仍能获得可靠的P值。经验贝叶斯调节的t统计量是limma差异表达分析的核心，它通过跨基因的信息共享，显著提升了小样本情况下检测差异表达基因的统计功效。

贝叶斯统计推断与B统计量

除了提供调节的t统计量和P值外，limma还计算一个贝叶斯对数几率统计量B（log-odds），用于从贝叶斯角度评估基因差异表达的证据。B统计量源于Lönnstedt和Speed（2002）提出的方法，其含义是“基因差异表达的对数几率”。具体而言，对于第j个基因的第k个系数，B统计量定义为：

B = log( (P_diff / P_non_diff) )

这里，P(基因j差异表达 | 数据)表示在给定数据下基因j差异表达的后验概率，P(基因j非差异表达 | 数据)则为非差异表达的后验概率。B统计量取对数形式，因此正值表示支持差异表达的证据更强，负值表示支持非差异表达的证据更强。当B_jk=0时，表示基因差异表达的后验概率为50%，即证据中立。

B统计量的计算依赖于经验贝叶斯框架下的先验假设。limma假设差异表达基因的对数倍数变化（logFC）服从一个先验分布，其方差由用户设定的参数控制（例如通过proportion参数指定差异表达基因的比例，通过stdev.coef.lim参数限定logFC的先验标准差范围）。基于这些先验，limma计算每个基因的后验概率，并进一步得到B统计量。值得注意的是，B统计量已经自动校正了多重检验，因为它在计算中考虑了先验的差异表达基因比例。因此，B统计量可以看作一个综合了效应大小和先验信息的指标，用于基因排序和筛选。

在实际应用中，B统计量与调节的t统计量及其P值通常提供相似的基因排序。然而，B统计量具有明确的概率解释，可以方便地转换为后验概率（例如，B=1.5对应约4.48:1的差异表达几率，即后验概率约82%）。此外，B统计量不受P值校正方法选择的影响，因为其本身已包含多重检验校正。因此，在一些分析中，研究者会参考B统计量来辅助判断基因差异表达的可靠性。

VisualBasic.NET中实现limma算法

limma的差异表达分析结果通常通过topTable函数提取，该函数返回一个数据框，其中每一行对应一个基因，每一列包含该基因的统计量和注释信息。下面的VB.NET对象定义了在R语言中的limma程序包的topTable函数所输出的数据框的列及其统计含义：

''' <summary>
''' limma ``topTable`` output dataframe.
''' </summary>
Public Class LimmaTable : Implements IDeg, INamedValue, IReadOnlyId, IStatPvalue

    ''' <summary>
    ''' row names - gene id
    ''' </summary>
    ''' <returns></returns>
    Public Property id As String Implements IDeg.label, INamedValue.Key, IReadOnlyId.Identity
    ''' <summary>
    ''' logFC（对数倍数变化）
    ''' </summary>
    ''' <returns></returns>
    ''' <remarks>
    ''' logFC表示基因在两组之间的对数倍数变化（log2 fold change）。对于简单的两两比较，
    ''' logFC等于处理组平均表达量减去对照组平均表达量（在log2尺度下）。
    ''' 例如，logFC=1表示处理组表达量是对照组的2倍（因为2^1=2），logFC=-1表示处理组表达量是对照组的一半。
    ''' logFC是差异表达分析中最直观的指标，用于衡量基因表达的上调或下调程度。
    ''' 需要注意的是，logFC的符号和大小依赖于实验设计和对比的设置，
    ''' 因此在多因素实验中应结合设计矩阵解读其含义。
    ''' </remarks>
    Public Property logFC As Double Implements IDeg.log2FC
    ''' <summary>
    ''' AveExpr（平均表达量）
    ''' </summary>
    ''' <returns></returns>
    ''' <remarks>
    ''' AveExpr表示该基因在所有样本中的平均表达水平（通常取log2 CPM或log2强度）。
    ''' AveExpr可用于评估基因的表达丰度，以及结合logFC判断差异变化的相对幅度。
    ''' 例如，一个logFC=2的基因，如果AveExpr很低（例如接近背景水平），则其实际上调倍数可能并不显著；
    ''' 反之，如果AveExpr很高，则logFC=2可能表示生物学上有意义的上调。
    ''' AveExpr在微阵列分析中常用于绘制MA图（M-A plot），其中M表示logFC，A表示AveExpr，
    ''' 以直观地展示差异表达与表达丰度的关系。在RNA-seq分析中，
    ''' AveExpr同样可用于质量控制和结果解释。
    ''' </remarks>
    Public Property AveExpr As Double
    ''' <summary>
    ''' t（经验贝叶斯调节的t统计量）
    ''' </summary>
    ''' <returns></returns>
    ''' <remarks>
    ''' t列即为经验贝叶斯调节的t统计量。它是logFC与其标准误差的比值，
    ''' 反映了logFC偏离零的程度相对于其估计误差的大小。t统计量越大（绝对值），
    ''' 表示logFC相对于其标准误差越大，即差异表达越显著。与常规t统计量不同，
    ''' 这里的t已经经过经验贝叶斯调节，其标准误差sj post融合了先验信息，
    ''' 因此在小样本情况下更稳定。t统计量服从自由度更高的t分布，其对应的P值即为P.Value。
    ''' 在解读时，t的符号与logFC一致，绝对值大小与P.Value呈负相关（|t|越大，P.Value越小）。
    ''' </remarks>
    Public Property t As Double
    ''' <summary>
    ''' P.Value（未校正的P值）
    ''' </summary>
    ''' <returns></returns>
    ''' <remarks>
    ''' P.Value是针对原假设“该基因无差异表达”计算得到的P值，基于经验贝叶斯调节的t统计量。
    ''' 具体地，P值通过比较调节的t统计量与其理论分布（t分布）获得，表示在原假设下观察到当前或更极端t值的概率。
    ''' 由于采用了经验贝叶斯调节，该P值在小样本情况下更加可靠。P.Value越小，表示拒绝原假设的证据越强，
    ''' 即基因差异表达的可能性越高。然而，由于成千上万个基因同时进行检验，
    ''' P.Value需要进行多重检验校正以控制错误发现率。
    ''' </remarks>
    <Column("P.Value")>
    Public Property P_Value As Double Implements IDeg.pvalue, IStatPvalue.pValue
    ''' <summary>
    ''' adj.P.Val（多重检验校正后的P值）
    ''' </summary>
    ''' <returns></returns>
    ''' <remarks>
    ''' adj.P.Val是对P.Value进行多重检验校正后的P值，用于控制错误发现率（FDR）或家族误差率（FWER）。
    ''' limma支持多种校正方法，其中最常用的是Benjamini-Hochberg（BH）方法，即控制FDR。
    ''' adj.P.Val表示在所有被宣布差异表达的基因中，预期假阳性的比例。例如，设定adj.P.Val阈值为0.05，
    ''' 意味着我们期望在所有选中的差异表达基因中，最多有5%是假阳性。adj.P.Val是筛选差异表达基因时的重要依据，
    ''' 通常选择adj.P.Val < 0.05作为显著性阈值。需要注意的是，adj.P.Val依赖于所选的校正方法和阈值，
    ''' 不同的校正方法（如BH、Bonferroni、Holm等）会得到不同的校正后P值。
    ''' </remarks>
    <Column("adj.P.Val")>
    Public Property adj_P_Val As Double

    ''' <summary>
    ''' B（贝叶斯对数几率统计量）
    ''' 
    ''' B统计量或log-odds，表示基因是差异表达的概率的对数；
    ''' 计算公式：B = log10( (1 - p) / p ) 其中p是基因是差异表达的概率，基于经验贝叶斯方法估计；
    ''' B统计量的数学意义：表示"基因差异表达的可信度"（B > 0表示有差异表达证据，B > 1表示强证据）。
    ''' </summary>
    ''' <returns></returns>
    ''' <remarks>
    ''' B列是贝叶斯对数几率统计量，表示基因差异表达的后验对数几率。B值综合考虑了效应大小（logFC）和先验信息，
    ''' 可以转换为后验概率来解释。例如，B=1.5表示基因差异表达的后验几率约为e^1.5=4.48:1，即后验概率约82%。
    ''' B值越大，表示支持差异表达的证据越强；B值越小（负值），表示支持非差异表达的证据越强。
    ''' B统计量已经内置了多重检验校正，因此可以直接用于基因排序和筛选。在实际应用中，
    ''' B值与P.Value通常提供一致的基因排序，但B值提供了概率解释，
    ''' 有助于在决策时结合生物学意义进行权衡。
    ''' </remarks>
    Public Property B As Double

End Class

基于上面的limma结果表格中的各个输出的列的定义，在GCModeller程序包构建了一个limma差异检验计算的方法模块。limma 的核心思想是利用经验贝叶斯方法对大量基因的方差信息进行“借用”和“收缩”，从而在小样本量下获得更稳定、更可靠的差异表达检验结果。下面，我将代码划分为六个主要的算法步骤模块，并结合 limma 的原理逐一讲解我们可以如何实现对R语言中的limma差异表达分析的核心流程的复现。

1. 数据预处理与设计矩阵构建

Dim control As Integer() = x.IndexOf(design.control)  ' 0
Dim treat As Integer() = x.IndexOf(design.experiment) ' 1
Dim xi As Double() = Replicate(0.0, control.Length) _
    .JoinIterates(Replicate(1.0, treat.Length)) _
    .ToArray
Dim rawX As Matrix = x

' transform the expression data to log2 scale
x = x.log(2)
design.ValidateSampleIDsHelper(control, treat)

代码首先根据实验设计 design，获取了对照组（control）和实验组（treat）样本在表达矩阵 x 中的列索引。由于 limma 的基础是线性模型。这里构建了一个最简单的设计矩阵 xi。对于对照组样本，其值为 0；对于实验组样本，其值为 1。这个向量 xi 就是线性模型中的自变量 X，它代表了我们要研究的实验条件变化。然后，我们在代码中对输入的矩阵x做了数据转换：x = x.log(2) 将原始表达量转换为 log2 标度。这是基因表达分析中非常关键的一步，通过log2变换，可以使倍数变化可加：在原始标度下，实验组是对照组的2倍，差值很大；但在 log2 标度下，log2(2A) - log2(A) = 1，差值恒定。这使得线性模型的系数（斜率）可以直接解释为 log2 倍数变化。同时，log2变换也可以稳定方差：基因表达数据通常存在均值-方差依赖关系（表达量越高，方差越大）。log 转换可以在一定程度上缓解这个问题，使其更符合线性模型的同方差假设。

2. 逐基因拟合线性模型

Dim logFC As Double() = New Double(x.size - 1) {}
Dim residuals As Double()() = RectangularArray.Matrix(Of Double)(x.size, control.Length + treat.Length)
Dim i As Integer = 0
Dim mean As Double() = New Double(x.size - 1) {}
Dim control_vs_treat As Integer() = control.JoinIterates(treat).ToArray

' 拟合线性模型（逐基因）
For Each gene As DataFrameRow In x.expression
    Dim y As Double() = gene(control_vs_treat) ' 获取该基因在所有样本中的表达值
    Dim lm As FitResult = LeastSquares.LinearFit(xi, y) ' 对 y 和 xi 进行线性拟合

    mean(i) = rawX(i)(control_vs_treat).Average
    logFC(i) = lm.Slope ' 斜率即为 logFC
    residuals(i) = lm.Residuals ' 残差

    i += 1
Next

在这个步骤中的线性拟合代码是 limma 分析的核心计算部分。代码对表达矩阵中的每一个基因独立地执行一次线性回归。

• 模型形式：拟合的线性模型为 y = β₀ + β₁ * xi + ε。
• y 是某个基因在所有样本中的 log2 表达量。
• xi 是我们之前构建的设计矩阵（0 和 1）。
• β₀ (截距) 代表了对照组的平均表达水平。
• β₁ (斜率) 代表了实验组相对于对照组的表达量变化。

基于上面的代码中所示的线性拟合结果，我们可以从中提取出一些关键统计量：

• logFC(i) = lm.Slope：这是最关键的参数。由于 xi 的取值是 0 和 1，斜率 β₁ 正好等于 (实验组均值 - 对照组均值)。因为数据在 log2 标度上，所以这个斜率就是 log2 倍数变化。
• residuals(i) = lm.Residuals：残差是观测值 y 与模型预测值 ŷ 之间的差值（ε = y - ŷ）。它代表了模型无法解释的随机误差。这些残差是下一步计算基因特异性方差的基础。

3. 经验贝叶斯方差调整

经验贝叶斯方差调整是 limma 方法论的灵魂，它使得 limma 在处理小样本量的转录组数据时，相比传统的 t 检验具有巨大的优势，能够得到更准确、更可重复的差异表达基因列表。

' 经验贝叶斯方差调整
' a vs b
Dim df_residual = (control.Length + treat.Length) - design.size
Dim gene_vars As Double() = residuals _
    .Select(Function(e) (New Vector(e) ^ 2).Sum / df_residual) _
    .ToArray

Dim prior_var As Double = gene_vars.Median
Dim prior_df = 4  ' limma默认先验自由度
Dim shrunk_vars = (prior_df * prior_var + df_residual * New Vector(gene_vars)) / (prior_df + df_residual)
Dim shrunk_se = Vector.Sqrt(shrunk_vars)

这是 limma 算法的在处理小样本检验的时候的精髓所在，也是它区别于普通 t 检验的关键。当我们在小样本量实验中（例如，每组只有3个重复），因为样本重复的数量很少的原因，对每个基因单独计算得到的方差（gene_vars）非常不稳定和不可靠。一个基因的方差可能被偶然地低估或高估，这会直接影响后续 t 检验的准确性。

所以为了解决掉这个小样本的数据处理问题，limma 提出了一个巧妙的假设：虽然每个基因的表达水平和变化程度不同，但大多数基因的方差应该在一个相似的范围内。因此，我们可以从所有基因的方差分布中估计一个“先验方差”（prior_var），然后用这个先验信息来“校正”或“收缩”每个基因的单独方差估计。

下面描述了上面的代码中所实现的这样子的方差调整的计算过程：

1. gene_vars：首先，根据每个基因的残差计算其样本方差（残差平方和 / 自由度 df_residual）。
2. prior_var：计算所有基因方差 gene_vars 的中位数作为先验方差的估计。中位数比均值更稳健，不易受到极端高表达或高变异基因的影响。
3. shrunk_vars：这是方差收缩的核心公式。它计算一个“收缩后”的方差，这个方差是基因自身方差和先验方差的加权平均。
   • 权重由各自的自由度决定：df_residual（样本量决定）和 prior_df（先验信息的权重，limma 默认为4）。
   • 当样本量很小（df_residual 很小）时，收缩会更倾向于先验方差 prior_var。
   • 当样本量很大时，收缩会更倾向于基因自身的方差 gene_vars。
4. shrunk_se：对收缩后的方差开平方，得到更稳定的标准误。

4. 计算 t 统计量与 p 值

' t检验与p值
Dim t_stats = logFC / shrunk_se
Dim df_total = prior_df + df_residual
Dim t As Vector = t_stats.Abs
Dim p_values = Hypothesis.t.Pvalue(t, df:=df_total, Hypothesis.Hypothesis.TwoSided)

从上一步骤中，我们有了可靠的效应大小估计（logFC）和更稳定的不确定性度量（shrunk_se），现在可以进行标准的假设检验了。上面的代码描述了在limma算法中的通过调整后的t检验方法过程：

1. t 统计量：t_stats = logFC / shrunk_se。t 统计量衡量的是效应大小（logFC）相对于其标准误（不确定性）的倍数。一个绝对值越大的 t 统计量，说明该基因的表达变化越显著，越不可能是随机波动造成的。
2. 自由度：df_total = prior_df + df_residual。这里的自由度也经过了经验贝叶斯的调整。它结合了样本自身的自由度和先验信息的自由度，反映了最终 t 统计量的不确定性程度。
3. p 值：根据计算出的 t 统计量和调整后的自由度 df_total，从 t 分布中计算出双尾检验的 p 值。p 值表示在“零假设”（即该基因在两组间无差异）成立的前提下，观测到当前或更极端的 t 统计量的概率。

5. 计算 B 统计量

Dim p0 As Double = 0.5 ' limma默认先验概率 (p0 = 0.5)
Dim BValues As Double() = New Double(logFC.Length - 1) {}

For offset As Integer = 0 To logFC.Length - 1
    ' B = log10( (1 - p) / p )
    ' 其中 p = p0 + (1 - p0) * (1 - p_value) / 2
    Dim p As Double = p0 + (1 - p0) * (1 - p_values(offset)) / 2

    If p > 0 AndAlso p < 1 Then
        BValues(offset) = std.Log10((1 - p) / p)
    Else
        BValues(offset) = Double.NaN ' 处理边界情况
    End If
Next

B 统计量是 limma 提供的另一个用于排序差异基因的指标，它基于贝叶斯思想。B 统计量本质上是对数后验几率。它试图回答一个问题：“在观测到数据后，这个基因是差异表达的概率是多少？” 实现这个B统计检验计算的计算逻辑如下所示：

1. p0 是先验概率，即在进行实验前，我们估计一个基因是差异表达的概率。limma 默认设为 0.5，表示我们认为一个基因是差异表达和非差异表达的可能性相同。
2. p 是一个基于 p 值计算的后验概率。公式 p = p0 + (1 - p0) * (1 - p_value) / 2 是一个将 p 值转换为后验概率的近似方法。p 值越小，这个后验概率 p 就越接近 1。
3. B = log10( (1 - p) / p ) 是对数几率 的计算。当 p > 0.5（即基因更可能是差异表达时），B 值为正；当 p < 0.5 时，B 值为负。B 值越大，表明基因是差异表达的证据越强。

与 p 值的区别：p 值是频率学派的概念，与样本量强相关。B 统计量则融入了先验概率，提供了一个更直观的“基因是差异表达的概率”的度量，有时被认为比 p 值更稳定。

6. 最终结果汇总与输出

For offset As Integer = 0 To logFC.Length - 1
    Yield New LimmaTable With {
        .logFC = logFC(offset),
        .id = x(offset).geneID,
        .P_Value = p_values(offset),
        .[class] = If(.P_Value < 0.05, If(.logFC > 0, "up", "down"), "not sig"),
        .t = t(offset),
        .AveExpr = mean(offset),
        .B = BValues(offset)
    }
Next

通过上面的几个主要的计算步骤中生成的临时变量，我们就拥有了可以构建出limma程序包的topTable函数的计算结果表格的信息：

• id: 基因标识符。
• logFC: log2 倍数变化，衡量差异的大小和方向（正值为上调，负值为下调）。
• AveExpr: 基因在所有样本中的平均表达量（这里用的是原始值的平均，但 limma 通常用 log2 值的平均）。
• t: t 统计量。
• P_Value: 经验贝叶斯调整后的 t 检验 p 值。
• B: B 统计量（对数后验几率）。
• class: 一个基于 p 值（如 < 0.05）和 logFC 符号的简单分类，用于快速筛选显著上调或下调的基因。

通过 Yield 关键字，我们在这里所实现的limma差异检验函数会为每个基因生成一个 LimmaTable 对象，最终形成一个完整的差异表达分析结果列表，方便后续进行筛选、可视化和生物学解释。

R#算法代码测试

最后，我们在这里可以通过集成在GCModeller程序包中的基因表达工具中的limma函数进行差异检验分析。以下的R#脚本为对所复现的limma函数方法的demo测试脚本：

require(GCModeller);

imports ["geneExpression" "sampleInfo"] from "phenotype_kit";

let expr_data = load.expr("expr_demo.csv");
let sampleinfo = sampleInfo(sample_id(expr_data), sample_id(expr_data));
let a_vs_b = make.analysis(sampleinfo, "Control", "Treat");

# "","Control","Control","Treat","Treat"
# "Gene1",3.46652611204643,3.55018762050146,7.70849594522328,7.7053469155135
# "Gene2",3.57034719401758,3.53504224429097,7.71013744320796,7.71200111719484
# "Gene3",3.47704718957051,3.35757734477259,7.70681151573607,7.69960103113447
# "Gene4",3.44785576750922,3.51384094937353,7.69978915728958,7.70750360623961

let deg = geneExpression::limma(expr_data, a_vs_b);

deg = deg[order([deg]::P_Value)];
deg = as.data.frame(deg);

print(deg, max.print = 20);

write.csv(deg, file = "limma_impl_degs.csv");

参考文献

1. Ritchie, M. E., et al. (2015). limma powers differential expression analyses for RNA-seq and microarray studies. Nucleic Acids Research, 43(7), e47.
2. Smyth, G. K. (2004). Linear models and empirical Bayes methods for assessing differential expression in microarray experiments. Statistical Applications in Genetics and Molecular Biology, 3(1), Article3.
3. Law, C. W., et al. (2014). voom: precision weights unlock linear model analysis tools for RNA-seq read counts. Genome Biology, 15(2), R29.
4. Smyth, G. K. (2005). Limma: linear models for microarray data. In: Bioinformatics and Computational Biology Solutions Using R and Bioconductor. Springer.
5. Lun, A. T., et al. (2016). RNA-seq analysis is easy as 1-2-3 with limma, Glimma and edgeR. F1000Research, 5, 1408.
6. Huber, W., et al. (2015). Orchestrating high-throughput genomic analysis with Bioconductor. Nature Methods, 12(2), 115-121.

• Author
• Recent Posts

谢桂纲

高级数据科学家 at 苏州帕诺米克

Working on Engineered bacteria CAD design on its genome from scratch. Writing scientific computing software for Tianhe & Sunway TaihuLight supercomputer. Do scientific computing programming in R/R# language, he is also the programming language designer of the R# language on the .NET runtime.

Latest posts by 谢桂纲 (see all)

• 建立KEGG的KO序列数据库 - 2026年1月4日
• 环境微生物群落GEMs建模综述 - 2025年12月29日
• 【虚拟细胞】翻译事件建模 - 2025年12月21日