文章阅读目录大纲
Sequence Logo 是一种可视化 DNA 或蛋白质序列保守性的图形表示方法。每个位置(列)上的字母堆叠高度代表该位点的信息含量(以 bits 为单位),而每个字母的高度则与其在该位点出现的频率成正比。高信息量的位置字母堆得高,低信息量的位置则矮甚至接近零。Sequence Logo的绘制遵循信息熵原理,我们可以很直观的通过某一个位置的总高低来了解该处位置的信息含量有多少,高信息量的位置,字母堆的高,一般会出现某一个字符特别高,表明该处非常保守。
位置权重矩阵(Position Weight Matrix, PWM)是描述基因组调控因子结合位点序列模式的核心模型。它通过统计在结合位点序列中每个位置上各核苷酸(或氨基酸)出现的频率,来量化该位置对不同碱基的偏好程度。PWM通常以矩阵形式表示,行对应核苷酸(A、C、G、T/U),列对应序列中的位置,矩阵元素即为该位置该核苷酸相对于背景的权重得分。这一模型简洁且易于计算,因此在转录因子结合位点(TFBS)等调控元件的识别和表征中被广泛采用。
构建PWM的第一步是确定背景频率,即在无选择压力情况下基因组中各核苷酸出现的概率。通常假设基因组中A、T、C、G四种碱基的背景频率相等(各为0.25),但在实际应用中也可根据具体物种或基因组区域的碱基组成进行调整。背景频率提供了比较基准:如果一个位置的碱基分布与背景无异,则该位置不提供信息;反之,如果某碱基在该位置显著高于或低于背景,则表明该位置对结合有偏好。
接下来,需要统计位点序列中各位置碱基的计数。假设我们有N条已知的结合位点序列,每条序列长度为L,那么对于第j个位置(j=1..L),可以统计出A、C、G、T在该位置出现的次数,分别记为 nA,j, nC,j, nG,j, nT,j 。这些计数除以总序列数N,即得到该位置各碱基的观测频率: pi,j = ni,j/N (i∈{A,C,G,T})。观测频率反映了在该位置上各碱基出现的相对比例。
信息熵与PWM位点权重计算
在得到观测频率后,可以计算每个位置的信息熵。信息熵是信息论中衡量随机变量不确定性的度量,在序列motif分析中用于量化一个位置碱基分布的不确定性。对于位置j,其熵 Hj 定义为:
Hj = -sum(p * log2(p))其中,pi,j为位置j上碱基i的观测频率。当该位置碱基分布完全随机(即四种碱基等概率)时,熵达到最大值(对于DNA为2 bits);当某碱基在该位置占绝对优势时,熵接近0,表示不确定性很低。
然而,直接使用观测频率构建权重矩阵会面临两个问题:一是某些位置可能出现零计数(即某碱基在该位置从未出现),导致对数计算无定义;二是小样本情况下观测频率可能偏离真实概率。为解决这些问题,通常引入伪计数进行平滑处理。伪计数是在每个计数上增加一个小的常数(例如1),从而避免零计数并降低小样本偏差。加入伪计数后,调整后的频率为:
p_prime = (n + alpha) / (N + sum(alpha))其中αi是对碱基i的伪计数(通常取αi = 1或根据背景频率按比例分配)。这样处理后,再计算熵和后续权重将更加稳健。
有了背景频率和调整后的观测频率,就可以计算位置权重矩阵的元素了。PWM的核心思想是计算每个位置上各碱基相对于背景的对数几率。具体而言,PWM的元素wi,j定义为:
w = log2(p_prime / p)其中pi是碱基i的背景频率,p'i,j是位置j上碱基i的平滑后频率。这个公式表示:如果某碱基在motif位置j的出现频率高于背景,则wi,j为正,表示该碱基在该位置被“偏好”;如果低于背景,则wi,j为负,表示该碱基在该位置被“回避”;如果与背景相同,则wi,j为0,表示该位置对该碱基无偏好。
通过上述计算,我们得到一个L×4的矩阵(L为motif长度,4为碱基种类),这就是位置权重矩阵。PWM能够为任意给定序列片段计算一个结合得分(PWM Score, PWMS),用于评估该片段与已知motif的相似程度。PWMS通常是将序列中每个位置对应碱基的PWM值相加得到:
PWMS = sum(w)其中sj是待评估序列在位置j的碱基。PWMS越高,表示该序列越符合motif的特征,即越可能是该调控因子的结合位点。

伪计数的选择对PWM有重要影响。过小的伪计数可能不足以消除零计数的影响,而过大的伪计数会过度“平滑”数据,使motif特征变得模糊。研究表明,对于常见样本量,伪计数取1左右往往能取得较好的平衡。此外,还有更复杂的正则化方法,如根据背景频率按比例分配伪计数,或使用Dirichlet先验进行贝叶斯估计,以进一步提高模型的稳健性。这些方法本质上都是在样本信息与背景先验之间取得权衡,从而得到更可靠的权重估计。
PWM作为描述序列motif的模型,具有简单直观、易于计算和解释的优点,在基因组学中被广泛应用。例如,在转录因子结合位点预测中,可以将PWM沿基因组滑动计算得分,以识别潜在的调控位点。在motif发现算法(如MEME、Gibbs采样等)中,PWM也是核心组件,用于迭代优化motif模型。
然而,PWM也存在一些局限。首先,它假设各位点之间相互独立,忽略了碱基之间的相关性。这在许多情况下并不成立,例如某些转录因子可能偏好特定的二核苷酸模式。其次,PWM对训练数据敏感,小样本或噪声数据可能导致模型偏差。为克服这些局限,研究者提出了扩展模型,如考虑位点间相关性的马尔可夫模型或贝叶斯网络,以及基于深度学习的模型等。尽管如此,PWM因其简洁性和可解释性,仍然是motif分析的基础和重要工具。
Sequence Logo的信息论基础
Sequence logo和PWM的原理深植于信息论。信息论由Claude Shannon于1948年创立,用于研究通信系统中信息的度量、压缩和传输。在生物学中,信息论的概念被广泛应用于序列分析,以量化DNA、蛋白质序列中蕴含的信息和不确定性。
信息熵与不确定性
信息熵是信息论的核心概念,用于度量一个随机变量的不确定性或信息量。对于离散随机变量X,其概率分布为p(x),则熵H(X)定义为:
HX = -sum(p * log2(p))熵的单位是比特(bits),表示要完全确定X的取值平均需要多少信息。当X的分布完全确定(即某个结果概率为1,其余为0)时,熵为0;当X的分布均匀随机时,熵达到最大值。例如,对于DNA序列的一个位置,如果四种碱基等概率出现,则该位置的熵为2 bits,表示完全不确定;如果只有一种碱基出现,则熵为0,表示完全确定。
在motif分析中,熵被用来衡量序列位置的保守性:保守位置对应低熵,可变位置对应高熵。通过计算每个位置的熵,我们能够量化motif中各位置的不确定性,从而识别出关键的保守位点。
相对熵与KL散度
相对熵,又称Kullback-Leibler散度,用于衡量两个概率分布之间的差异。对于离散分布P和Q,相对熵D(P||Q)定义为:
DPQ = sum(P * log2(P/Q))相对熵总是非负的,且当且仅当P=Q时为0。它表示用分布Q来近似分布P时所损失的信息量,或者P相对于Q的“信息增益”。
在motif分析中,相对熵常用于计算信息含量。将motif位置j的碱基分布视为P,背景分布视为Q,则D(P||Q)即等于该位置的信息含量Rj。这体现了信息论与motif分析的深刻联系:motif的信息含量实际上就是motif分布相对于背景分布的相对熵。
信息含量与序列保守性
信息含量(IC)结合了熵和相对熵的概念,用于量化序列motif的保守程度。一个motif的总信息含量是其各位置信息含量之和,反映该motif相对于背景的整体信息增益。高信息含量意味着motif序列模式高度保守,与背景差异显著;低信息含量则表示motif接近背景随机序列,保守性弱。
信息含量的计算依赖于背景模型的选择。如果背景是均匀分布,则IC等于最大熵减去实际熵;如果背景非均匀,则IC等于相对熵。无论哪种情况,IC都提供了一个统一的度量来比较不同motif的保守强度,以及评估motif在基因组中的显著性。
信息论在motif分析中的意义
信息论为motif分析提供了坚实的理论基础和工具。首先,它将序列模式抽象为概率分布,使我们能够用数学语言描述和比较motif。其次,信息论概念(如熵、相对熵)直接对应于motif的保守性和特异性,为motif的发现、比较和可视化提供了量化指标。例如,Sequence logo正是基于信息含量来绘制高度,从而直观地呈现motif的信息结构。
此外,信息论还启发了许多高级分析方法。例如,互信息(Mutual Information)可用于检测motif中位点之间的相关性,从而发现更复杂的序列模式;最小描述长度(MDL)等原理可用于motif模型选择,避免过拟合。可以说,信息论是理解序列motif的“语言”,它帮助我们解读DNA序列中蕴含的调控信息。
Sequence logo绘制原理
Sequence logo是一种将PWM或频率矩阵可视化的图形表示方法,由Schneider和Stephens于1990年提出。它通过直观的图形展示motif中每个位置的信息含量和碱基组成,成为生物学和生物信息学中展示序列模式的标准方式。Sequence logo的成功在于其简洁性和清晰性:一图胜千言,能够快速传达motif的保守性特征和变异模式。
信息含量(IC)的计算
Sequence logo的核心是每个位置上各碱基字母的高度,该高度由该位置的信息含量(Information Content, IC)决定。信息含量衡量了该位置相对于背景的保守程度,单位为比特(bits)。对于位置j,其信息含量Rj定义为:
Rj = Hmax - Hj = log2(4) - Hj = 2 - Hj其中Hj是位置j的熵(如前述计算),Hmax是最大可能熵(对于DNA为2 bits,对应完全随机分布)。因此,Rj表示该位置碱基分布相对于背景所减少的不确定性,即该位置提供的信息量。如果某位置完全保守(只有一种碱基出现),则Hj=0,Rj=2 bits,表示该位置提供了2 bits的信息;如果某位置碱基分布与背景无异,则Hj=2 bits,Rj=0,表示该位置未提供任何信息。
需要注意的是,上述计算隐含假设背景是均匀分布。如果背景频率不均等,则信息含量的计算应采用相对熵(Kullback-Leibler散度)形式:
Rj = sum(p[i,j] * log2(p[i,j]/p[i]))这实际上就是PWM在该位置各碱基权重之和,也等于该位置的相对熵。当背景不均匀时,使用相对熵可以更准确地衡量motif相对于背景的信息增益。
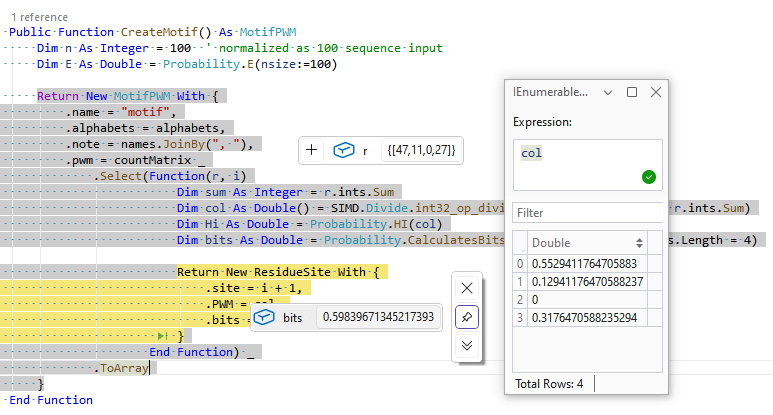
在下面的VB.NET代码中,我们实现了上面描述的这样子的一个针对PWM中各个位置的信息含量Bits的计算:
Dim n As Integer = 100
' normalized as 100 sequence input
Dim E As Double = Probability.E(nsize:=n)
Dim isNtMol As Boolean = alphabets.Length = 4
Return New MotifPWM With {
.name = "motif",
.alphabets = alphabets,
.note = names.JoinBy(", "),
.pwm = countMatrix _
.Select(Function(r, i)
Dim sum As Integer = r.ints.Sum
Dim col As Double() = SIMD.Divide.int32_op_divide_int32_scalar(
r.ints, r.ints.Sum)
Dim Hi As Double = Probability.HI(col)
Return New ResidueSite With {
.site = i + 1,
.PWM = col,
.bits = Probability.CalculatesBits(Hi, E, NtMol:=isNtMol)
}
End Function) _
.ToArray
}
Public Shared Function HI(col As IEnumerable(Of Double)) As Double
Dim h As Double = Aggregate n As Double
In col
Into Sum(If(n = 0R, 0, n * Math.Log(n, 2)))
h = 0 - h
Return h
End Function
''' <summary>
''' The information content (y-axis) of position i is given by:
'''
''' ```
''' Ri = log2(4) - (Hi + en) // nt
''' Ri = log2(20) - (Hi + en) // prot
''' ```
'''
''' 4 for DNA/RNA or 20 for protein. Consequently, the maximum sequence conservation
''' per site Is log2 4 = 2 bits for DNA/RNA And log2 20 ≈ 4.32 bits for proteins.
'''
''' </summary>
''' <param name="En">e_n = \frac{1}{2 \ln(2) \cdot n}</param>
''' <param name="NtMol">
''' calculate for the nucleotide sequence model?
''' </param>
''' <returns></returns>
Public Shared Function CalculatesBits(Hi As Double, En As Double, NtMol As Boolean) As Double
' Math.Log(n, 2) - (h + en)
' log2(4)=2, log2(20)≈4.32
Dim maxInfo As Double = If(NtMol, 2, Math.Log(20, newBase:=2))
Dim bits = maxInfo - (Hi + En)
' 信息含量不能为负(理论上最小为0)
Return std.Max(0, bits)
End Function字母高度与排列
在得到每个位置的信息含量Rj后,Sequence logo将该位置的总高度设为Rj(单位bits)。然后,在该位置垂直堆叠各碱基字母,每个字母的高度由其在PWM中的权重(或频率)决定。具体而言,字母i在位置j的高度hi,j通常取:
h[i,j] = p[i,j] * Rj其中pi,j是位置j上碱基i的频率(或平滑后频率)。这意味着字母高度正比于其频率:出现频率越高的碱基,在该位置堆叠中占据的高度越大。同时,各字母按照频率从高到低在堆叠中自下而上排列,最常见碱基位于堆叠顶部,次常见碱基紧随其下,依此类推。这种排列方式使得观察者一眼即可看出该位置的共识碱基(堆叠顶部的字母)以及各碱基的相对丰度。
需要注意的是,由于Rj可能小于最大值2 bits,实际堆叠总高度可能小于2 bits。当某位置信息含量较低(接近0)时,堆叠高度很矮,表示该位置几乎不保守;当信息含量较高(接近2 bits)时,堆叠高度接近2 bits,表示该位置高度保守。这种高度的可变设计使得Sequence logo能够直观反映motif不同位置的保守程度差异。
Logo的可视化效果

通过上述方法,Sequence logo将PWM的数值信息转化为直观的图形。观察一个典型的DNA motif logo,可以看到:
- 保守位点:高度保守的位置在logo中表现为高耸的堆叠,顶部往往只有一种碱基字母,表示该位置几乎所有序列都使用同一碱基。例如,许多转录因子结合位点的核心识别位点在logo中呈现为尖锐的“山峰”。
- 可变位点:可变位置则堆叠较矮,可能包含多种碱基字母,表示不同序列在该位置使用不同碱基。例如,一些位置可能允许两种碱基交替出现,在logo中表现为两个字母各占约一半高度。
- 信息含量:整个logo的总高度(所有位置堆叠高度之和)反映了该motif的总信息量,可用于评估motif的特异性强度。信息含量越高的motif,其序列模式越明确,在基因组中出现的偶然概率越低。
Sequence logo不仅适用于DNA序列,也可用于蛋白质序列的motif可视化。在蛋白质logo中,20种氨基酸字母按照频率和保守性进行堆叠,同样能够揭示功能域或结合位点的保守特征。
绘制代码的实现
现在假设我们有下面的一个用来表示motif绘制的PWM矩阵的数据模型,用来用作为整个 motif 的容器:
Public Class DrawingModel
' PWM矩阵
Public Property Residues As Residue()
Public Property En As Double
Public Property ModelsId As String
End Class
Public Class Residue
' 包含该位点所有可能字符(如 A/T/G/C 或 20 种氨基酸)及其相对频率。
Public Property Alphabets As Alphabet()
' 该位点的信息含量(bits)
' 这个值决定了该列的总高度。通常由 PWM 计算得出
' 最大为 log₂(4)=2 for DNA,
' log₂(20)≈4.32 for protein)。
Public Property Bits As Double
Public Property Position As Integer
End Class
' 存储单个碱基或氨基酸及其频率。
Public Class Alphabet
Public Property Alphabet As Char
' 计算当前字母在图中的实际绘制高度 = RelativeFrequency * Ri
'(即频率 × 该列总高度)
Public Property RelativeFrequency As Double
End Class基于PWM矩阵所来源的分子序列类型,我们可以定义出Y坐标轴:
' n=4(DNA) or 20(AA)
Dim maxBits As Double = Math.Log(n, newBase:=2)
' Y轴
' 最大信息量 maxBits = log₂(字母表大小)。
' 绘制 Y 轴(从 0 到 maxBits)
Call g.DrawLine(Pens.Black, New PointF(X, Y - yHeight), New PointF(X, Y))然后我们就可以在代码中,通过遍历每个位点(Residue)进行Sequence Logo图中的每一列的绘制
Dim source As IEnumerable(Of Residue) = If(reverse,
model.Residues.Reverse,
model.Residues)
For Each residue As Residue In source
' ...
yHeight = region.Height * (Min(residue.Bits, maxBits) / maxBits)
If Not frequencyOrder Then
order = residue.Alphabets
Else
order = (From rsd As Alphabet
In residue.Alphabets
Order By rsd.RelativeFrequency Ascending).ToArray
End If
' 按频率升序(底部到顶部)
For Each alphabet As Alphabet In order
If alphabet.RelativeFrequency <= 0 Then Continue For
Dim H As Single = alphabet.RelativeFrequency * yHeight
Y -= H ' 向上移动(因Y轴向下)
g.DrawImage(colorSchema(alphabet.Alphabet), X, Y, wordSize, H)
Next在上面所绘制的每一个残基位置处的字符是通过colorSchema中预渲染的字符图片的在高度上的拉升来实现的。对于出现频率高的字符,其对应的H会比较高,则对应的字符的预渲染的字符图片的高度拉升会比较高,在Sequence Logo中的显示会比较高。在colorSchema之中,默认是使用下面的颜色配色来进行预渲染:
DNA 颜色(经典配色):
A: Green
T: Red
G: Yellow
C: Blue
Protein 颜色(按化学性质分类着色):
酸性(D/E): Coral/Cyan
碱性(R/K/H): Black/Yellow/Gold
疏水(A/I/L/M/F/W/V): CadetBlue/HotPink/LightSlateGray 等
极性(N/Q/S/T/Y): Chocolate/LawnGreen/RoyalBlue/SkyBlue下面的表格为我们总结了假若你想要自己编写一个Sequence Logo的绘制代码,所需要的一些关键步骤:
| 步骤 | 实现目的 | 代码实现 |
|---|---|---|
| 1. 输入模型 | 数据准备 | DrawingModel 包含 Residue[],每个 Residue 有 Alphabet[] 和 Bits |
| 2. 计算列高 | 信息含量 | Bits 直接决定列总高度(归一化到画布) |
| 3. 计算字母高 | 字母高度 | H = RelativeFrequency * Bits |
| 4. 堆叠顺序 | 视觉层次 | 按频率升序绘制(低频在底,高频在顶) |
| 5. 颜色映射 | 生物学意义 | ColorSchema 提供 DNA/Protein 预设配色 |
| 6. 坐标轴 | 可读性 | 绘制 Y 轴(bits 刻度)、X 轴(位点编号)、"Bits" 标签 |
| 7. 渲染输出 | 图形引擎 | 使用 GDI+ 绘制预渲染字母图像 |
DNA Motif 示例解析
为了更直观地理解Sequence logo的绘制原理,下面以一个简化的示例进行说明。假设我们有一个长度为6的DNA motif,包含5条序列:
位置: 1 2 3 4 5 6
序列1: A G C T A C
序列2: A G C T A C
序列3: A G C T A C
序列4: A G C T G C
序列5: A G C T G C首先统计各位置碱基计数(这里假设背景均匀,伪计数取0):
位置1:A=5, C=0, G=0, T=0
位置2:A=0, C=0, G=5, T=0
位置3:A=0, C=5, G=0, T=0
位置4:A=0, C=0, G=0, T=5
位置5:A=3, C=0, G=2, T=0
位置6:A=0, C=5, G=0, T=0计算各位置熵和信息含量:
- 位置1:只有A出现,H1=0,R1=2 bits
- 位置2:只有G出现,H2=0,R2=2 bits
- 位置3:只有C出现,H3=0,R3=2 bits
- 位置4:只有T出现,H4=0,R4=2 bits
- 位置5:A出现3次,G出现2次,H5 = -[3/5*log2(3/5) + 2/5*log2(2/5)] ≈ 0.971 bits,R5 = 2 - 0.971 ≈ 1.029 bits
- 位置6:只有C出现,H6=0,R6=2 bits
接下来,根据频率分配各字母高度:
位置1:A占100%,高度=2 bits(堆叠顶部为A,总高2 bits)
位置2:G占100%,高度=2 bits(堆叠顶部为G,总高2 bits)
位置3:C占100%,高度=2 bits(堆叠顶部为C,总高2 bits)
位置4:T占100%,高度=2 bits(堆叠顶部为T,总高2 bits)
位置5:A占60%,G占40%,高度分配:A=0.6*1.029≈0.617 bits,G=0.4*1.029≈0.412 bits(堆叠总高≈1.029 bits,顶部为A,下方为G)
位置6:C占100%,高度=2 bits(堆叠顶部为C,总高2 bits)最终,该motif的Sequence logo将显示为:前4个位置和第6个位置都是高耸的单字母堆叠(A、G、C、T、C),第5个位置稍矮,顶部为A、下方为G。这样的图形直观地告诉我们:该motif在前4位和第6位高度保守,第5位允许A或G,但偏好A。通过这个简单示例,可以清楚地看到Sequence logo如何将PWM的数值信息转化为高度和字母排列,从而揭示motif的序列模式。
使用GCModeller绘制Sequence Logo
在GCModeller之中,提供了一个用于发现序列中的保守pattern的程序包,在这个程序包中提供了从输入的fasta序列使用吉布斯方法进行motif扫描,以及motif的两个导出操作:sequence logo的绘制以及motif结果的表格导出操作。下面的R#脚本展示了如何通过GCModeller程序,从输入序列的fasta数据到生成motif数据,最后进行sequence logo的绘制的过程:
require(GCModeller);
imports "bioseq.patterns" from "seqtoolkit";
imports "bioseq.fasta" from "seqtoolkit";
# read sequence data and found motif via gibbs scan method
let raw = read.fasta("Staphylococcaceae_LexA___Staphylococcaceae.fasta");
let motif = gibbs_scan(raw, width = 18);
# draw sequence logo of the generated motif
bitmap(file = "LexA.png") {
plot.seqLogo(motif, title = "LexA");
}
svg(file = "LexA.svg") {
plot.seqLogo(motif, title = "LexA");
}
pdf(file = "LexA.pdf") {
plot.seqLogo(motif, title = "LexA");
}
#cast motif data result as dataframe and export to table file
motif = as.data.frame(motif);
motif = motif[order(motif$score),];
print(motif, max.print = 13);
write.csv(motif, file = "LexA.csv");
参考文献列表
- Schneider, T.D., & Stephens, R.M. (1990). Sequence logos: a new way to display consensus sequences. Nucleic Acids Research, 18(20), 6097-6100.
- Crooks, G.E., Hon, G., Chandonia, J.M., & Brenner, S.E. (2004). WebLogo: a sequence logo generator. Genome Research, 14(6), 1188-1190.
- Bailey, T.L., Boden, M., Buske, F.A., Frith, M., Grant, C.E., Clementi, L., Ren, J., Li, W.W., & Noble, W.S. (2009). MEME Suite: tools for motif discovery and searching. Nucleic Acids Research, 37(Web Server issue), W202-W208.
- Nettling, M., Treutler, H., Grau, J., Keilwagen, J., Posch, S., & Grosse, I. (2015). DiffLogo: a comparative visualization of sequence motifs. BMC Bioinformatics, 16, 387.
- Xia, X. (2012). Position Weight Matrix, Gibbs Sampler, and the Associated Significance Tests in Motif Characterization and Prediction. Scientifica, 2012, 917540.
- Workman, C.T., Yin, Y., Corcoran, D.L., Ideker, T., Stormo, G.D., & Benos, P.V. (2005). enoLOGOS: a versatile web tool for energy normalized sequence logos. Nucleic Acids Research, 33(Web Server issue), W389-W392.
- Olsen, L.R., Kudahl, U.J., Simon, C., Sun, J., Schönbach, C., Reinherz, E.L., Zhang, G.L., & Brusic, V. (2013). BlockLogo: Visualization of peptide and sequence motif conservation. Journal of Immunological Methods, 400-401, 37-44.
- Christen, F., & Nielsen, M. (2012). Seq2Logo: a method for construction and visualization of amino acid binding motifs and sequence profiles including sequence weighting, pseudo counts and two-sided representation of amino acid enrichment and depletion. Nucleic Acids Research, 40(Web Server issue), W281-W287.
- Menzel, P., Seemann, S.E., & Gorodkin, J. (2012). RILogo: visualizing RNA–RNA interactions. Bioinformatics, 28(19), 2523-2526.
- Vacic, V., Iakoucheva, L.M., & Radivojac, P. (2006). Two Sample Logo: A Graphical Representation of the Differences between Two Sets of Sequence Alignments. Bioinformatics, 22(12), 1536-1537.
- Maddelein, D., Colaert, N., Buchanan, I., Hulstaert, N., Gevaert, K., & Martens, L. (2015). The iceLogo web server and SOAP service for determining protein consensus sequences. Nucleic Acids Research, 43(Web Server issue), W543-W546.
- Vinga, S. (2014). Information theory applications for biological sequence analysis. Briefings in Bioinformatics, 15(3), 376-389.
- Stormo, G.D. (2013). Consensus patterns in DNA. Methods in Enzymology, 525, 211-221.
- Altschul, S.F., et al. (1997). Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Research, 25(17), 3389-3402.
- 单细胞视角下的微生物基因组代谢酶嵌入分析 - 2026年2月25日
- 基因组代谢酶层级嵌入 - 2026年2月23日
- 基因组功能吉布斯LDA主题建模 - 2026年2月23日


No responses yet